нетривиални проблеми на вероятностите

С една дума: ". Откриват се средната площ на проекцията на куб с ръб с дължина 1, върху равнина с изотропно разпределена случайна посока на проекция" С други думи, това, което е средното очаква площ от куба на всички възможни ориентации?

Тази публикация изследва използването на Mathematica, да се разбере, и в крайна сметка реши проблема. Тя пресъздава ми решение на този проблем.

Проекцията на площада в права линия

Преди да се пристъпи към случая на кутията, аз започнах с единицата площ, случайно завъртане около центъра на масата, с намерението да намери своята проекция на средната дължина на хоризонталната ос.

За простота, аз поставя в центъра на масата в района на произход.

Намерени лявата и дясната страни на издатината като най-малките и най-големите х координират върховете на квадрата, въртящи се около произхода от ъгъл а:

след това се комбинира тези функции в манипулират [], за да може да се променя динамично ъгъл на въртене:

Това е очаква дължината като функция на ъгъла на въртене:

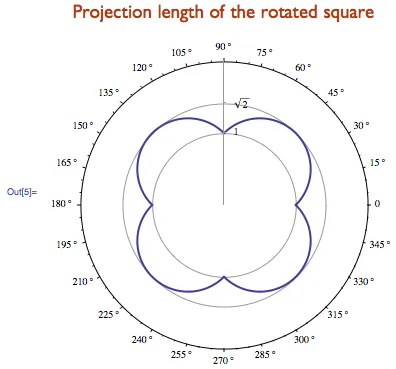
Ако приемем, че ъгълът на въртене α е равномерно разпределена в интервала 0 ≤ алфа