необходимия минимум
1.Dispersiya
Дисперсия - характеристики на случайни величини, определени като очакването на площада на отклонението на случайна променлива от неговото очакване.
Теоретично вариацията е мярка за разпространението на разпределението на вероятностите. Тя се определя като очакването на квадрат разликата между стойността на


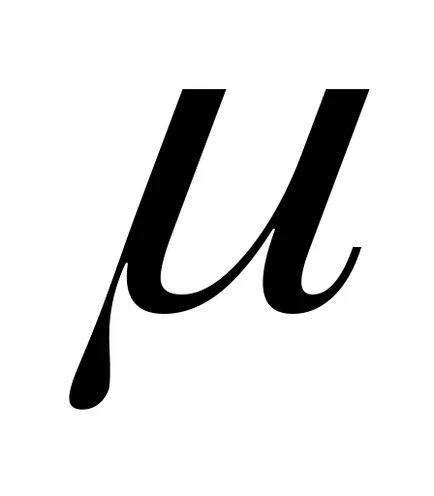


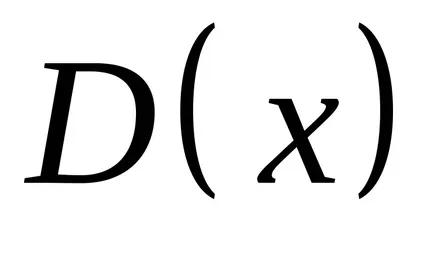
.
от
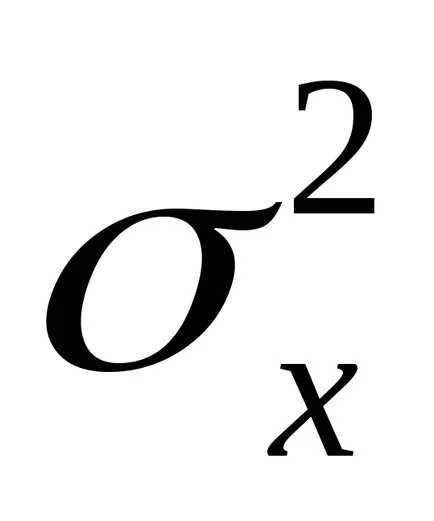

стойност



2.Mat. очакване
Очакванията - сумата на продукти от стойности на случайна променлива до съответните вероятности.
Очакванията на дискретна случайна променлива - е претеглена средна стойност на всички възможни стойности, където тегловен коефициент се приема като вероятността от съответния изход. Можете да го изчисли, като се умножи всички възможни стойности на случайна променлива на тяхната вероятност и сумиране на получения продукт. Математически, ако случайна променлива е определен като


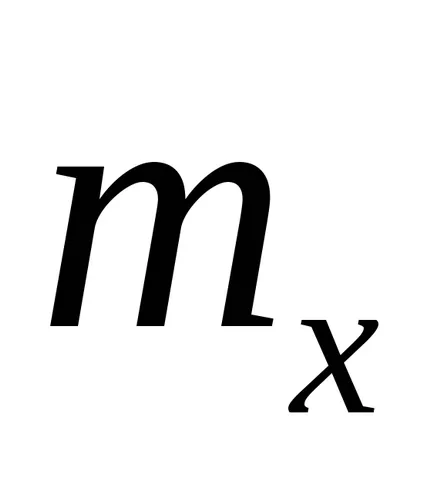
Да предположим, че
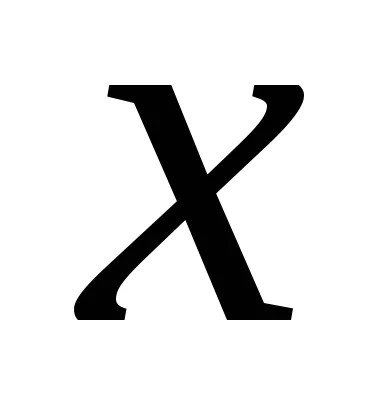


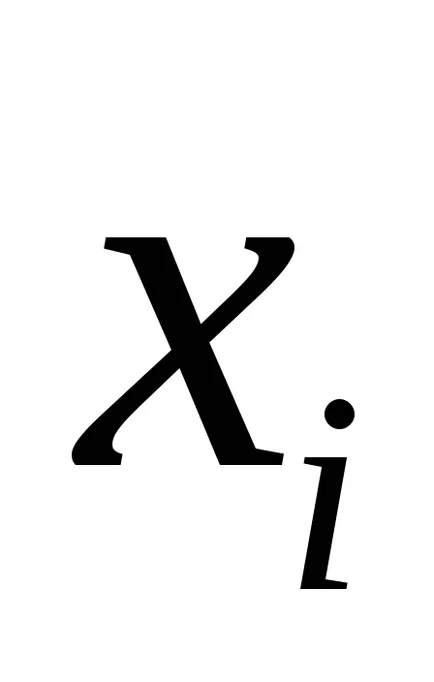

.
Математическият очакване на случайна променлива е често по-нататък нейната средна над цялото население. За случайна променлива
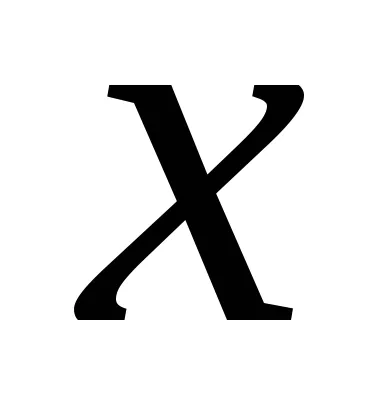

Очакванията на дискретни случайни величини функции
нека

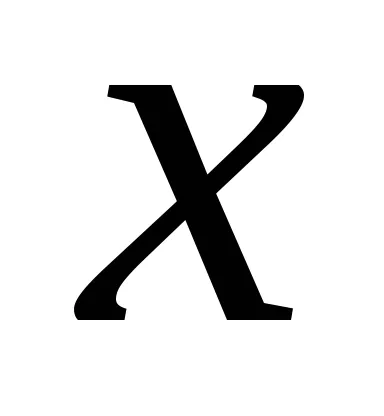


,
където сумирането е над всички възможни стойности

Правила за изчисляване на математическото очакване
Има три правила, които често се използват. Тези правила са почти очевидни, и те са еднакво приложими за дискретни и непрекъснати случайни величини.
Правило 1. Очакването на сумата от няколко променливи е равен на сумата от техните математически очаквания. Например, ако има три случайни величини



.
Правило 2. Ако случайна променлива се умножава с константа, а след това му очаквания се умножава по една и съща константа. ако
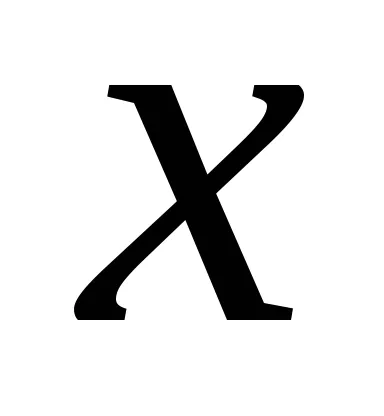

.
Правило 3. очакването за постоянно там себе си. Например, ако

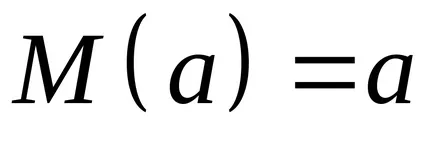
Разследването на трите правила:
.
Ковариация - числова характеристика на съвместна дистрибуция на две случайни величини, равни на очакването на продукта на отклонения на случайни величини от техните математически очаквания.
Може да се използват следните готови формули, които следват директно от разтвора на системата (1.4):
където - ковариация признаци





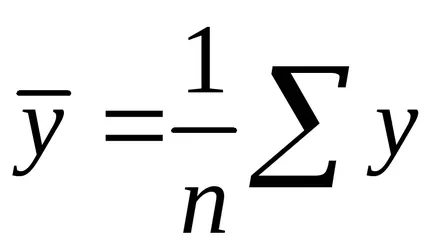


4.Korrelyatsiya
Коефициентът на корелация или коефициент на корелация двойка - мярка за промените в характера на две случайни величини. Коефициентът на корелация е обозначен с латинска буква
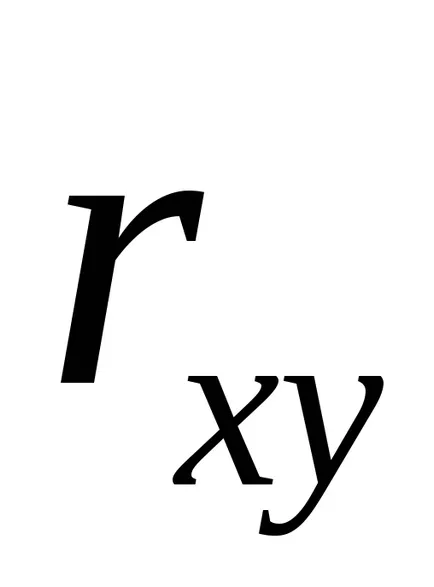
Уравнението на регресия винаги се допълва от близостта индикатор за връзката. При използване на линейна регресия като индикатор на такива действия коефициент линейна корелация
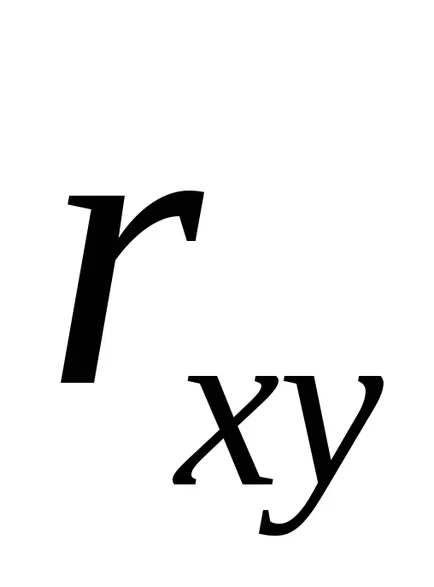
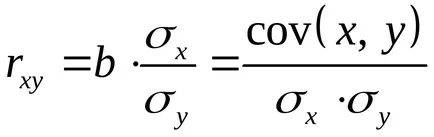
Коефициентът на линейна корелация е в границите:
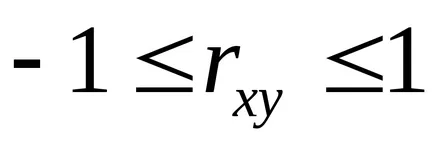

За да се оцени качеството на избора на линейна функция се изчислява квадрат на коефициента на линейна корелация
