Намирането на най-малко предварително определена целева функция
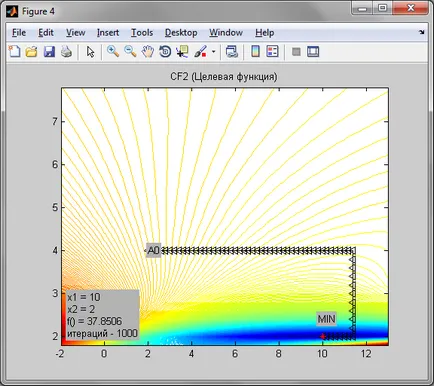
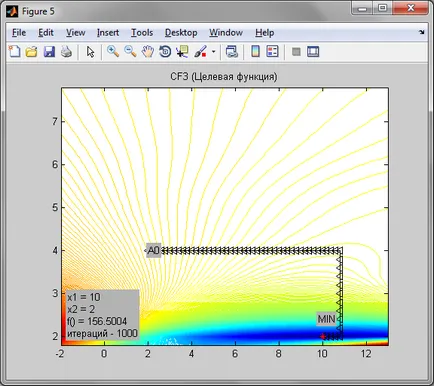
Поради факта, че методът на нулев ред на спускане, това е доста точна. Поради факта, че функцията за Rosenbrock има клисура помощ да достигне минималната точка не успя. спиране точка в този случай е доста далеч от минимум точка. В случай на минималната точка функция елипса се постига в 21 итерация, при стъпка з = 0.2. Въпреки това минимално точка предварително определена цел функция беше постигнато точно 91 на повторение, със стъпка з = 0.2, и с точност от 0.0001.
библиография
основния файл на проекта.
4. ITERATION_AMOUNT = 1000;
5. ЕПСИЛОН = 0.001; % точност
7. POINT_AMOUNT = 50; % Брой на точки
9% отправна точка
11. x_point_Ellipse (1) = 2;
12. x_point_Ellipse (2) = -2;
14. x_point_Rosenbrock (1) = 4;
15. x_point_Rosenbrock (2) = 3;
17. a1_T_point_CF (1) = 2;
18. a1_T_point_CF (2) = 4;
20.% А и В - стойностите за радиуси F-II. Ellipse.
24% първоначалните настройки функция W (и).
28. ELLIPSE = 'ELLIPSE;
29. ROSENBROCK = 'ROSENBROCK;
32. Част 1% Ойлер.
33. y_teor = FirstPart_EulerMethod (a1, Т, POINT_AMOUNT);
35% Част 2 coordinatewise оптимизация.
36.% функция [value_of_funct, X] = SecondPart_OptimizationCoordinate (function_name, Н, ЕПСИЛОН, ITERATION_AMOUNT, а, Ь, y_exp, number_y_exp, POINT_AMOUNT)
37. [y_Ellipse, x_Ellipse] = SecondPart_OptimizationCoordinate (елипса, Н, ЕПСИЛОН, ITERATION_AMOUNT, x_point_Ellipse, а, Ь, 1, 1, POINT_AMOUNT);
38. [y_Rosenbrock, x_Rosenbrock] = SecondPart_OptimizationCoordinate (ROSENBROCK, Н, ЕПСИЛОН, ITERATION_AMOUNT, x_point_Rosenbrock, а, Ь, 1, 1, POINT_AMOUNT);
40% част 3. RNG. CF
41. [CF, a1_T_1, a1_T_2, a1_T_3] = ThirdPart (CF_text, Н, ЕПСИЛОН, ITERATION_AMOUNT, a1_T_point_CF, а, Ь, y_teor, POINT_AMOUNT);
Функцията на метода на Ойлер.
1. функция y_Euler_50point = FirstPart_EulerMethod (a1, Т, POINT_AMOUNT)
3. глобалната y_Euler;
5. ITERATION_AMOUNT = 300; % Броят на точките за първи график.
6. x_t = 5; % От постоянна връзка х (т)
11. coeff_z1 = 120 * а1 / T. ^ 2 + 6;
12. coeff_z2 = 6 * a1-120 + 48 * а1 / Т;
13. coeff_x_t = 120 * а1 / T. ^ 2;
14.% free_term - без план.
15. free_term = coeff_x_t * x_t;
17. за I = 1: ITERATION_AMOUNT
18. z1 (I + 1) = Z1 (I) + Н * z2 (I);
19. z2 (I + 1) = z2 (I) + Н * (x_t-z1 (I) -0,4 * T * z2 (I)) / T. ^ 2;
20. y_Euler (I) = coeff_z1 * z1 (I) + coeff_z2 * z2 (I) - free_term;
24.% I = 1: ITERATION_AMOUNT;
26.% заглавието ( "Y графика на теоретичните точки 300. ');
28.% SaveAs (GCF, "изход", "BMP);
29% от резерва от 300 точки само 50 (POINT_AMOUNT)
31. step_cycle = ITERATION_AMOUNT / POINT_AMOUNT;
32. за I = 1: step_cycle: ITERATION_AMOUNT
33. y_Euler_50point (J) = y_Euler (I);
38.% I = 1: POINT_AMOUNT;
40.% заглавието ( "Y теоретично графика 50 точки (всеки 6). ');
Функция coordinatewise оптимизация
1. Част 2% coordinatewise оптимизация.
2. функция [value_of_funct, X] = SecondPart_OptimizationCoordinate (function_name, Н, ЕПСИЛОН, ITERATION_AMOUNT, x_start_point, а, Ь, y_exp, number_y_exp, POINT_AMOUNT)
8. ясно (varlist);
14. Преместване%. да пропуснете условията на изпитване извън предх. value_of_funct мин на последните три или не.
15. change_coord = 1;
16%, за да излезете контура ако броят. Повече повторения ITERATION_AMOUNT.
17. number_iteration = 1;
23. х (1,1) = x_start_point (1); Първо% координира, първата стойност.
24. х (2,1) = x_start_point (2); Второ% координира, първата стойност.
25. х (1,2) = х (промяна, I-1) + Н; Първо% координира, втора стойност.
26. х (2,2) = х (константа, I-1); Второ% координира, втора стойност.
28. value_of_funct (1) = Ellipse_Rosenbrock_or_CF (function_name, х (1,1) х (2,1), а, Ь, y_exp, number_y_exp, POINT_AMOUNT);
29. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, х (1,2) х (2,2), а, Ь, y_exp, number_y_exp, POINT_AMOUNT);
31. ако new_value_of_function> value_of_funct (1)
33. х (1,2) = х (промяна, I-1) + Н;
34. value_of_funct (2) = Ellipse_Rosenbrock_or_CF (function_name, х (промяна, I), X (константа, I), а, Ь, y_exp, number_y_exp, POINT_AMOUNT);
37. value_of_funct (2) = new_value_of_function;
40% цикъл, докато абсолютната стойност на разликата функционира по-голяма прецизност епсилон и броя на повторенията е по-малко от ITERATION_AMOUNT (10000).
41. а (ABS (value_of_funct (I) -value_of_funct (I-1))> ЕПСИЛОН (number_iteration 43. number_iteration = number_iteration + 1; 45. change_coord = change_coord + 1; 47% добавите стъпка към първата координата. 48. х (промяна, l) = х (промяна, I-1) + Н; 49% втора координатна пренаписване. 50. х (постоянни, I) = х (константа, I-1); 51% се намери стойността на функцията на новите стойности. 52. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, х (1 I), X (2, I), а, Ь, y_exp, number_y_exp, POINT_AMOUNT); 54%, ако функцията на настоящите стойности на повече от една функция на предходната, след з = H + (-1). друго value_of_funct (I) = new_value_of_function. 55. ако new_value_of_function> value_of_funct (I-1) 57% нула, последната стойност 58. х (промяна, l) = NaN; 59. I = I - 1; % Да се върнете към предишната функция на минималната стойност % 62. Ако положението на смяна крачка направена не по-малко от 3 точки, след като направи мин value_of_funct от последните 3. стойности. 63. ако (change_coord> = 3) 65%, ако функцията на стойностите на предишната стъпка е по-малко ток и по-малко, отколкото в етап I-2, след това да промените координира движението. 66. ако value_of_funct (I-1)> = value_of_funct (I) 68. След% Промяна координира темпо - zeroize change_coord. 69. change_coord = 0; 70. ако (константа == 1) 16. value_of_funct = сума ((y_exp (number_y_exp, :) - y_model) ^ 2) / POINT_AMOUNT ;. 20. value_of_funct = 1;