Начини за решаване на алгебрични уравнения
- полином уравнение на форма PN на (X) = 0, където Pn (х) - N-та степен полином по отношение на х;
- дробни рационални уравнения, т.е. съдържащ два компонента като частни две полиноми;
- ирационално уравнение.
За редица техники са малко теоретична обосновка. 30 показва техниките илюстрирани повече от 36 примери. Не мислете, че се има предвид в конкретния пример, на рецепцията е най-рационалното решение за този пример. Просто трябва да се вземат под внимание наличието на такъв подход за решаване на уравнения.
Същият подход (използването на тригонометрията, използването на хомогенност, факторинг и др) се използват не само в работата си с рационалното, на рационални, ирационални уравнения, но и в решаването на някои класи уравнения, неравенства, системи.
Тези ползи могат да бъдат намерени достатъчно на брой уравнения, необходими, разбира се, без да се пренебрегват други източници.
1. Ние докаже теоремата: Ако уравнение х п + п е -1x -1 + ... + a1x + a0 = 0 (*) с цели коефициенти има рационален корен, където р и р са относително прости, след a0 неделими от стр. и разделен от р.
Доказателство: Ние замести в (*) х нататък. получи правилната числено равенство, умножим двете страни с р п:
Дясната страна се дели на р. Следователно, отляво трябва да се дели от р. но тъй като р и р са относително прости, тогава р п не е неделими от р. но тогава трябва да се дели от р. друго лявата ръка не се дели на р.
Дясната ръка е кратно на стр. Следователно, ляво кратно на стр. но р п са относително прости за стр. след a0 е кратно на стр. Това доказва теоремата.
Доказателство: Дивидентът е равна на делителя умножен по коефициент плюс остатъка. Тъй като делител - първа степен полином, остатъкът ще бъде полином чиято степен е по-малка от тази на средствата делител, остатъкът - CONST. Коефициент е полином от степен п - 1. След това,
Когато X = на това уравнение има формата
от което следва, Р (а) = R. теорема.
Следствие: Ако X = а - корен на полином, полином е разделена от х - че няма остатък.
Доказателство: Ако уравнение х = а (***) става 0 + R. = 0, което означава, че R = 0. И тъй като останалата част от разделянето е нула, тогава твърдението е доказано.
Пример 1. решаване на уравнението 30x 4 + х 3 - 30x 2 + 3 х + 4 = 0.
Състав на различни фракции неделими чиито числители - делители на постоянен план, т.е. 4 и знаменатели - водещи коефициент делители, т.е. 30.
В лявата колона в знаменателя включва всички делители на 30. Очевидно е, че - 1 - корените на полином. Като следствие от теорема Bezout разделение полином при х + 1
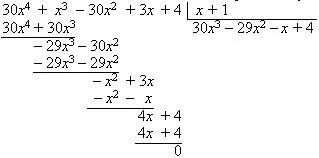
За корените на полином 3 30x на - 29x 2 - х + 4 използването фракции масата. Когато полином под формата Следователно, - основата на полином.
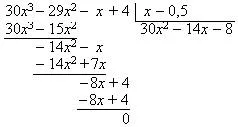
2. При решаването алгебрични уравнения може да бъде полезен метод за неопределени коефициенти.
Пример 2: решаване на уравнение х 4 + 2х 3 - 16x 2 + 11x - 2 = 0.
Нека полинома представени като продуктът
където. б. гр. а. б. в коефициенти, които са желателно избрани така, че след разширяване скоби и редуциращи условия, сходни превърнати оригиналния полином. Ние премахване на скобите, приемайки, че а = а = 1.
Нека с = 1, G = - 2 или с = 2, G = - (1 изберете коефициенти).
б = - 3, б = 5 след това.
Ние твърдим, че б = 5, гр = - 2, В = - 3, с = 1. Този набор отговаря на всички четири уравнения, така че можем да запишем
След като решила квадратно уравнение, ние откриваме корените на оригиналното уравнение.
3. С решението за повтарящи уравнения
След терминът от термин разделен от х к. те са решени чрез заместване на
Пример 3. 4 решаване на уравнението 2х - 3x 3 - 7х 2 -15x + 50 = 0.
Разделя се на х 2. получи
Уравнението е следното:
Ако л = 1, тогава уравнението на форма ос на + 2k 2k -1 BX + СХ + DX -2 2k 2k + -3 ... + DX 3 + CX 2 + BX + а = 0, се нарича връщане (или симетричен) чрез уравнението на първия вид на степен 2k ,
Пример 4. решаване на уравнението 4 + 3x 5х 3 - 16x 2 + 3x + 5 = 0.
Ние разделяме план със срок от х 2. Ние имаме.
Ако L = - 1, ние получаваме уравнението на формата
брадва + 2k 2k -1 BX + СХ + DX -2 2k 2k + -3 ... + DX 3 + CX 2 - BX + а = 0, което се нарича връщане (или симетричен) 2k степен уравнение на втория вид. То се решава чрез заместване на
Пример 5 решаване на уравнение 8x 4 - 42x 3 + 2 + 29x 42x + 8 = 0.
Палиндромната полином от нечетен степен има корен - 1. Това се дължи на факта, че уравнението има четен брой членове, при заместване на X от - 1 двойки са унищожени. Ето защо, в началото на полинома е разделен от х + 1, и частното ще доведе до връщане на уравнението дори степен, решение, което вече е било обсъдено.
Пример 6. решаване на уравнението 5 24x + 74x 4 - 123x 3 - 123x 2 + 74x + 24 = 0.
Имаме палиндромна полином петата степен. Един от корените - 1. Чрез разделяне от х + 1, получаваме
Според Нютон binomu
Забележка 2. Определяне на външния вид, че уравнението е завръщането не винаги е лесно, особено ако. Ето защо, в уравнението на степен 2n ние произвеждаме termwise разделение на х н и, ако това дава сума от изрази. където п = 0, 1, 2, ... m. След това по-нататъшно решение е ясно.