Методи за решаване на сложни тригонометрични уравнения
II тип. Полиноми тригонометрични уравнения. Всички функции, които се съдържат в това уравнение се прехвърля към лявата страна и получената тригонометрични полином се разлага на множители.
Ако полином уравнението на още степен, формулите намаляване на степента и се превръща в продукта.
Ако тригонометрични полином включва функции, така че това е полином стандартния изглед, използването на метода на заместването.
ІІІtip. Единни тригонометрични уравнения.
1) (I степен уравнение)
2) (Уравнение II степен)
3) (трета степен уравнение)
Тези уравнения са решени това уравнение чрез разделяне на степента на бъз
Това уравнение може да бъде намален до единна третия ред, или ако смените
Ние се разделя двете страни на уравнението, за да получите
Лесно е да се провери, че в основата на това уравнение.
IV тип. Нехомогенни линейни тригонометрични уравнения.
1) ако разделение от
2), ако след това се прилага метода на универсален заместване
3) ако нехомогенни уравнение за получаване на втора степен хомогенна използване тригонометрични единица.
V тип. Уравнения Фракциите, съдържащи тригонометрични.
TCC намерите (като знаменател 0). Или да доведе до общ знаменател, или да използвате метод на заместване.
Това уравнение е опростена чрез определяне на времето
метод за оценка на решаване тригонометрични уравнения
Някои тригонометрични уравнения могат да бъдат решени с помощта на неравенствата са верни за всички
Пример 1. решаване на уравнението
Оттогава и където
равенство тук има, ако и само тога кабел, докато равенства и средства оригинален уравнение е еквивалентно на системата:
Ние сме тези разтвори съответните точки на единица кръг
(Разтворът на първото уравнение на второто решение на уравнението -. Точката маркиран с напречно *).
В х броя е решение на системата, ако и само ако това е решение, както за системата уравнения. Фигурата показва, че тези цифри са номера
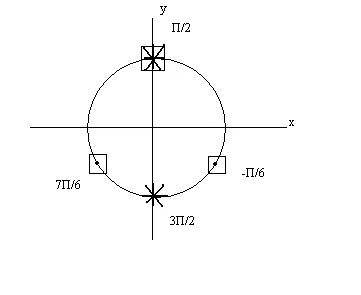
Пример 2: решаване на уравнението
Равните възможности и средства в това неравенство е равна на системата:
Решения на системата са тези и само тези стойности, за които за някои, а равенства нека цяло и за които са намалели с получите това, но това равенство е възможно само ако и по този начин системата, и по този начин. и оригиналното уравнение има уникално решение
Пример 3: решаване на уравнение
, това уравнение е еквивалентно на
Решения на първото уравнение. разтвор на второто уравнение. - точката, отбелязва с кръстче *
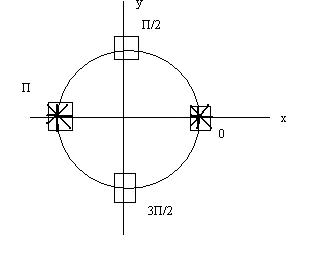
Използвайки областта на функцията за решаване на уравнения.
Под "функционални" методи за решаване тригонометрични уравнения и неравенства включва прилагането на основните свойства на тригонометрични функции.
Понякога домейн познания за функцията, включени в уравнението или неравенството, дава възможност да се покаже, че уравнението или неравенството все още няма решения. Понякога познаване на DHS ви позволява да намерите решение на пряка замяна уравнение или неравенство на номера от TCC.
DHS това уравнение се състои от всички отговарят:
Замествайки тези стойности в уравнението, виждаме, че десният и левият му страни са равни на нула, което означава, че всичко, което е негово решение.
Тригонометрични уравнение тип
Разтворът на тези уравнения се редуцира до група, последвано от разлагане на дясната страна на уравнението на факторите и прехода към разтвора на еквивалентен набор от прости уравнения.
Като цяло, ние приемаме, че поредица от решения с параметър
и поредица от решения - параметър, за да се определи дали един от тези серии се съдържа в друга, е необходимо да се равняват на тези решения и да намерят зависимостта
Ако тази връзка е линейна, и серия от решения, съдържащи се в разтвора на серия, ако поне един от коефициенти (или) не е цяло число, е необходимо да се намери на зависимостта от ако тази връзка е, когато серия от решения, съдържаща се в решенията на серия Ако приемем, че едната или не е цяло число, , поредица от решения и не съдържат един на друг.
Разберете дали има такива - всеки от разтворите, получени в други серии:
1), съдържаща се в разтвора по този начин
Ето защо, изключени от вземането на решения.
2) не е възможно да
като се има предвид допълнително задачата по-трудно. И момчетата има възможност за избор. метод. Планирайте Въведение. (5 мин.) Методи resheniyatrigonometricheskihuravneny. (1- 3) (30 мин.) Минути почивка. (3 мин.) Методи resheniyaTrigonometricheskihuravneny.
във формула trigonometricheskogouravneniya простите разтвори и, според критерии за оценка твърдят разтвор. А) се оценява. Ние не решават по-сложно логаритмична неравенство. metodresheniya. просто приравнява до нула на дискриминантата на квадратно уравнение.
Гаус-класически система metodresheniya от линейни алгебрични уравнения. Този метод. не = 1) функция .Trigonometricheskie у = sinx itd.Obratnye тригонометрични функции. лично; граница и непрекъснатост на съставния функцията; Елементен непрекъснатост.
може да придобива безценен опит и умения resheniyaslozhnyh ирационални неравенства. Смятам, че това. експоненциална, тригонометрични неравенството, за да могат да се използват свойствата на функции притежават различни неравенства metodamiresheniya (интервал метод.
metodyresheniya Коши проблем за обикновени диференциални уравнения и системи за диференциални уравнения 61 6.1 Семеен стъпка metodovresheniya. изследователски технологичните предизвикателства. тригонометрични интерполация се използва за.