Местно и неразделна Лаплас Теорема
Е необходимо да се изчисли: а) очакването М (X), Ь) дисперсия D (X), в) стандартно отклонение сигма.
Решение. а) математически очакването М (X) на дискретна случайна променлива X е сумата от двойки продуктите на всички възможни стойности на случайната променлива съответстваща на вероятността от възможни стойности. Ако X е дискретна случайна променлива определена маса (1), след това очакването М (X) се изчислява по формулата
Очакванията на М (X) се нарича също така средната стойност на случайна променлива X. Използване на (2), ние получаваме:
б) Ако М (X) е математически очакването на случайна променлива X, разликата X-М (х) е отклонението на случайна променлива X е средната стойност. Тази разлика характеризира разсейването на случайната променлива.
Дисперсията (разсейване) на дискретна случайна променлива X е математически очакването (средна стойност), квадратно отклонение на случайната променлива от очакването. По този начин, по дефиниция, ние имаме:
Изчисляваме всички възможни стойности на квадрат отклонения.
За да се изчисли дисперсията D (X), образуване на разпределение право квадратен отклонение и след това се прилага с формула (2).
Сега ние откриваме математическата очакването M (X 2).
М (х 2) = (48) 2 ∙ 0,2 + (53) 2 ∙ 0,4 + (57) 2 ∙ 0,3 + (61) 2 ∙ 0,1 =
Прилагайки (4), получаваме:
D (X) = 2931,2- (54) 2 = 2931,2-2916 = 15,2.
Както можете да видите, имаме един и същ резултат.
в) промяна на размер е квадрата на случайна променлива величина. Следователно, за характеристиките на разсейване на възможните стойности на случайна променлива около своята средна стойност по-удобно да се разгледа степента на която е равна на средната аритметична стойност на корен квадратен от дисперсията, т.е.
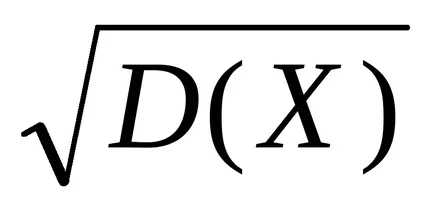
Прилагайки (5), ние имаме: σ =
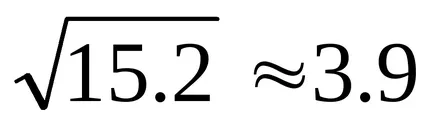
Пример. В случайна променлива X има нормално разпределение. Очакванията на М (X) = 5; dispersiyaD (X) = 0,64. Виж вероятността резултат от теста ще има стойност х в интервала (4, 7).
Решение. Известно е, че ако случайна променлива X е избран диференциална funktsieyf (х), вероятността, че X приема стойността принадлежащи на интервала (α, β), изчислена по формулата
Ако стойността на X има нормално разпределение, диференциална функция
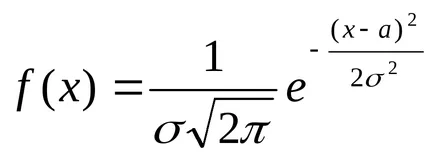
където = М (X) и σ =
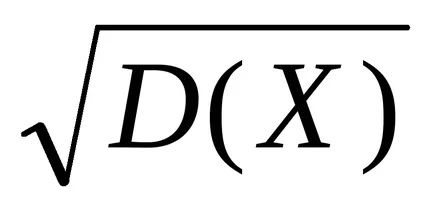
Формула (2) могат да бъдат трансформирани, използвайки функцията Лаплас.
Направи заместването. нека
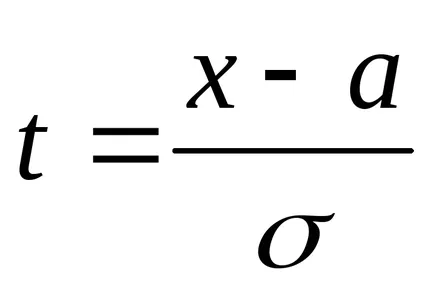
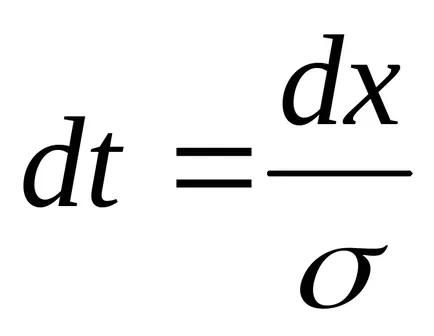
Следователно gdet1 IT2 подходящи граници за peremennoyt.
Намаляване на σ, ние имаме
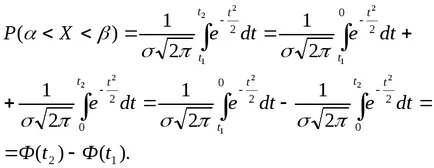
Смяна на наложеното
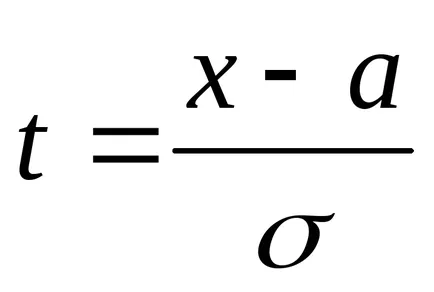
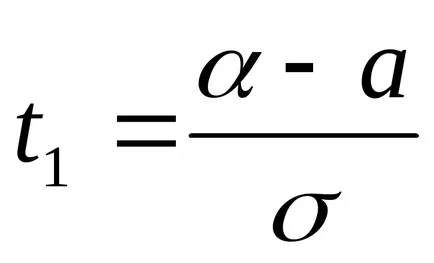
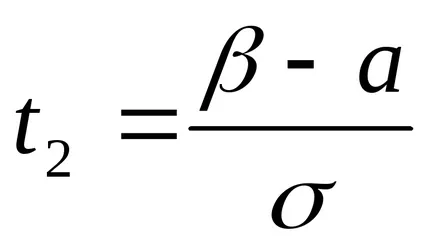
Чрез хипотеза имаме проблем: а = 5; σ =
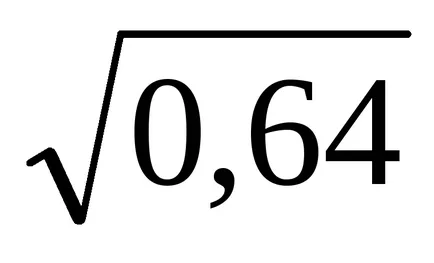
Пример. Смята се, че дължината на отклонение от стандарта на произведените части е разпределена случайна променлива обикновено. Стандартни дължина (очакване) а = 40 cm, стандартното отклонение σ = 0,4 см. Вижте вероятност, че отклонението от стандартната дължина ще бъде абсолютната стойност на не повече от 0.6 cm.
Решение. Ако X - дължината на елементите, тогава състоянието на проблема, тази стойност трябва да бъде в интервала (а-δ, а + δ), където а = 40 и δ = 0,6.
Поставянето на формула (3) α = а-δ и β = а + δ, получаваме
Замествайки в (4) наличните данни, които получаваме:
Следователно, вероятността, че фабричните артикули с дължина ще бъде в диапазона от 39,4 до 40.6 cm е 0.8664.
Пример. Диаметър на части, произведени растение, е разпределена случайна променлива обикновено. Diametraa стандартна дължина = 2.5 cm, стандартното отклонение σ = 0,01. В рамките на това, което граници почти може да се гарантира, дължината на диаметъра на частта, ако се приемат като значимо събитие, вероятността за което е равно на 0,9973?
Решение. Чрез хипотеза имаме проблем:
Прилагането на формула (4), ние получаваме:
Съгласно Таблица 2, ние откриваме, че такава стойност на функцията на Лаплас има X = 3. Ето защо,
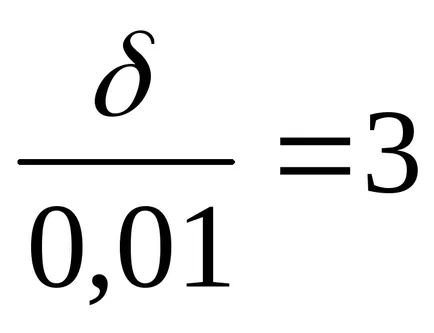
По този начин, ние можем да гарантираме, че дължината на диаметъра ще варира от 2.47 до 2.53 cm.