Matrix алгебра - транспонирана матрица
Matrix алгебра - транспонирана матрица

редове съответно колони дава т.нар транспонирана матрица измерение п х m:

По-специално, за strokitransponirovannoy вектор-матрица е вектор колона
Основните свойства на транспонирана матрица:
1) два пъти транспонирана матрица съвпада с оригинала:
2) сумата от транспонирана матрица на матрици, е равна на сумата от транспонирана матрица на условия, т.е.
3) транспозицията на матрица продукта от матрици е продукт на транспонирани матрични фактори, взети в обратен ред:
За квадратна матрица има очевидни равенство:
Ако матрицата съвпада с неговата транспозиция
той се нарича симетрична. От последния уравнение следва, че симетрична матрица е квадратна и неговите елементи са симетрични около главния диагонал са равни:
Очевидно е, че продуктът е симетрична матрица като използването на имот 3, получаваме:
ПРИМЕР Пример. Предвид матрица А и транспозиция на матрицата:
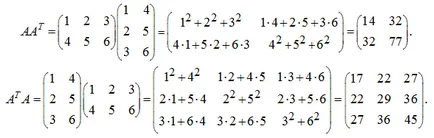
Както може да се очаква, получил симетрични матрици.