Математическа статистика 2, решаване по математика и така нататък проблем.

1. При проучването на структурата на търговските банки, обявени в уставния капитал на три хиляди банки в страната са били избрани от самата схема на случайна извадка от сто повторение-безплатно. Данните за разпределението на банките на тази основа са представени в таблицата по-долу:

А) вероятността, че средният размер на уставния капитал на търговските банки се различава от средната стойност на размера му в пробата е не повече от пет милиона рубли (в абсолютна стойност);

В) количеството на повторение без проба, в която същото отклонение на средната големина на капитал на всички банки (не повече от пет милиона рубли вж. A)), той може да бъде осигурена с вероятност от 0.95.

а) Намерете средният размер на уставния капитал според средната претеглена стойност на формула:

Стандартното отклонение на процентното намаляване на разходите:

Вероятността, че средният размер на уставния капитал на търговските банки се различава от средната стойност на размера му в пробата е не повече от пет милиона рубли:

. В) количеството на повторение без проба, в която същото отклонение на средната големина на капитал на всички банки (не повече от пет милиона рубли виж точка а)), той може да бъде осигурена с вероятност от 0.95:

Към 0.95. след това

2. В съответствие с предходната задача, трябва да:

А) се предположи, модел, който се доближава до емпиричната разпределение, информиран избор;

В), използвайки # 967; 2 - критерий Pearson, при ниво на значимост а = 0,05 за тестване на хипотезата, че случайна променлива X - размера на уставния фонд на нормално разпределение.

Построява се хистограма на един чертеж и съответните емпирични нормално кривата на разпределение.

Оформете спомагателна таблица за изчисляване на теоретичните честоти:

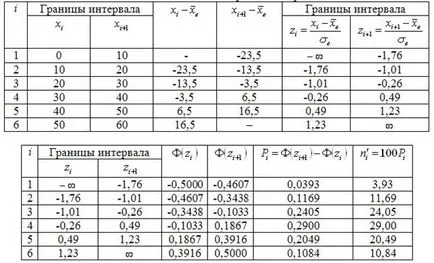
Нека сравним емпирични и теоретични честоти:

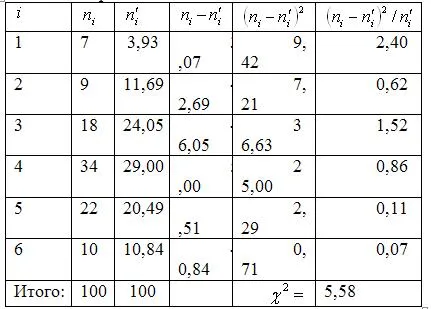
Чрез разпределение таблица на критичните точки # 967; 2 за степента на значимост # 945; = 0.05 и броят на степените на свобода. Изчислената стойност е по-малка от масата, следователно, с вероятност от 95% може да се твърди, че случайна променлива X - размер на разрешените средства - нормално разпределение.

Хистограмата на емпиричното разпределение и съответната нормална крива:

При фактора 0,95 доверие е 1.96. след това

За да тествате хипотезата за равенство на дела на зрителите под 0.41 конкуриращи хипотези.

, тогава няма причина за отхвърляне на нулевата хипотеза, че е, резултатите от проучването не са случайни.

4. Разпределение на петдесет фирми в размерите на дълготрайни активи (X милиона рубли) и изходна база (милиона), дадени в таблицата по-долу:

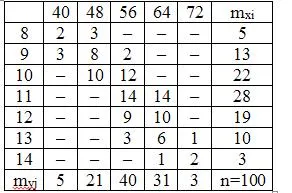
А) изчисляване на групата означава и емпирични конструиране на регресионната линия;

В) се предполага, че между променливите х и у, има линейна корелация:

- намерите уравнението на регресия линии, за конструиране на техните графики в една цифра с емпирични регресионни линии и получаване на икономически тълкуването на получените уравнения;

- изчисли корелационен коефициент, при ниво на значимост = 0.05 цената му стойност и сключва стягане и посока връзка между променливите х и у;

- в случай на отхвърляне на хипотезата за отсъствие на изходния обем корелация от размера на ДМА за оценка на мярката за размер ефект на ДМА в размер на изход (да се използва коефициент на определяне и съотношение корелация);

-използване на съответния регресионно уравнение за изчисляване на средната мощност на предприятия, дълготрайните материални активи на 81 милиона рубли ..

емпирична регресия линия на Y на X:

емпирична регресия линия на X на Y:

Създаване на масата за уреждане (на най-долния ред на работите):

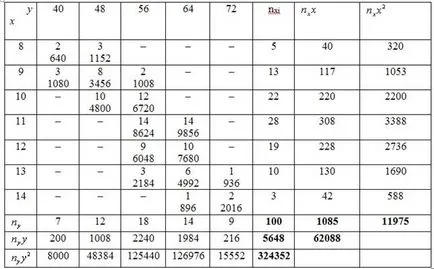
Ние считаме, средната на извадката: