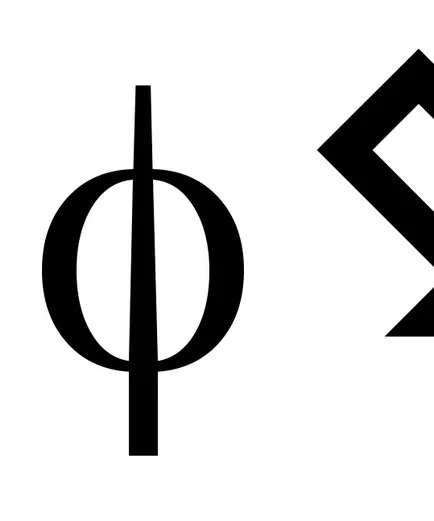
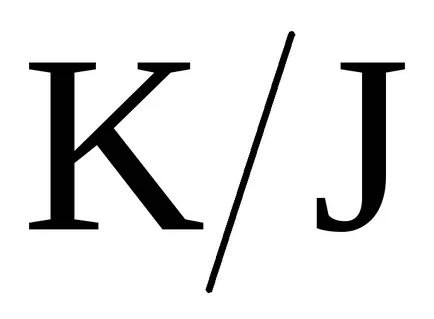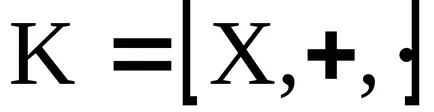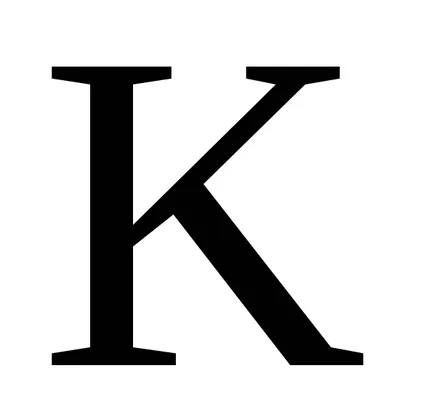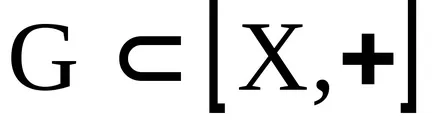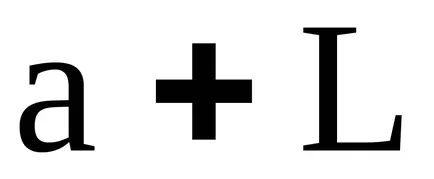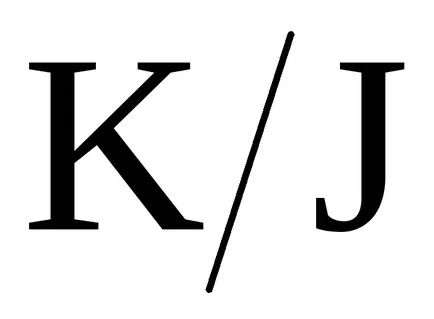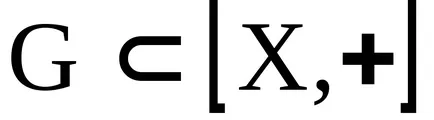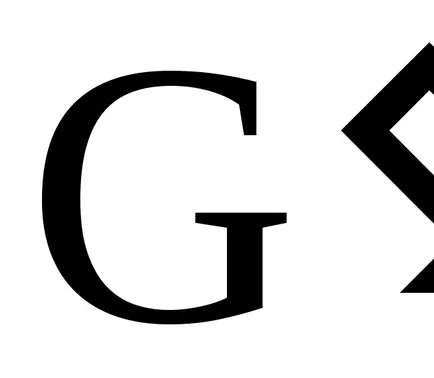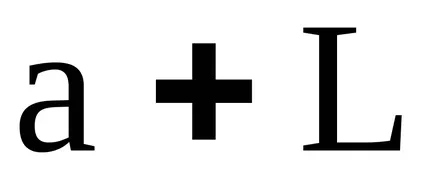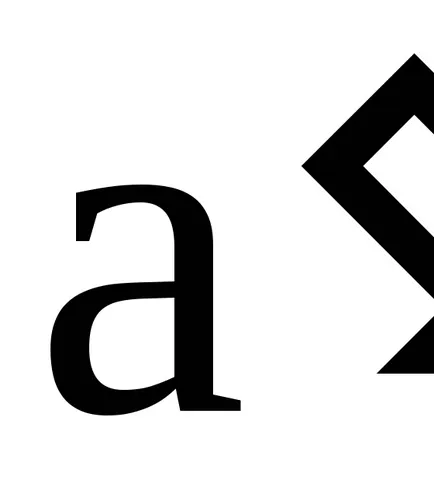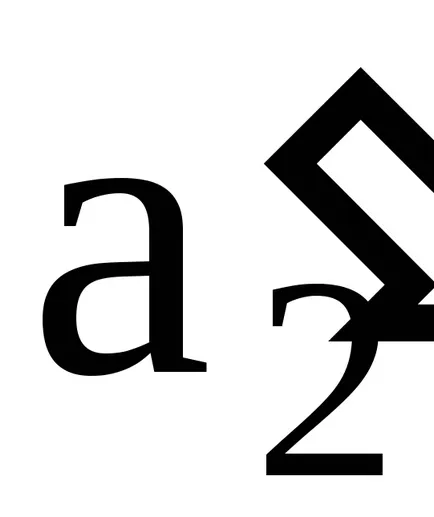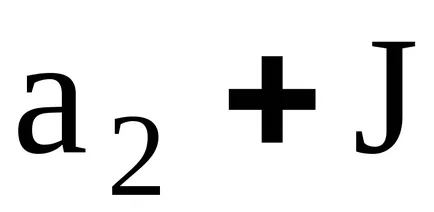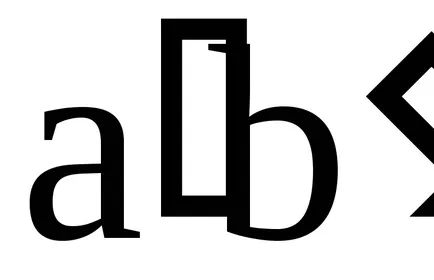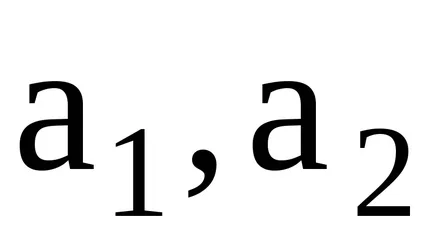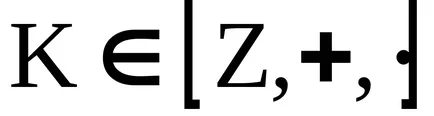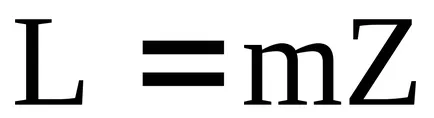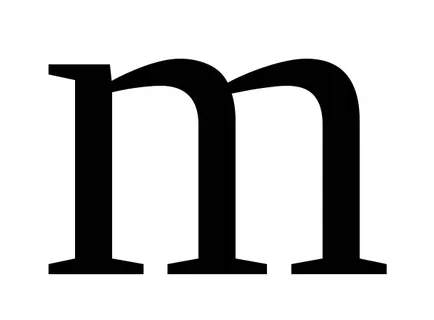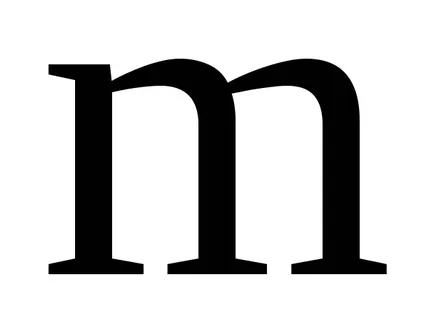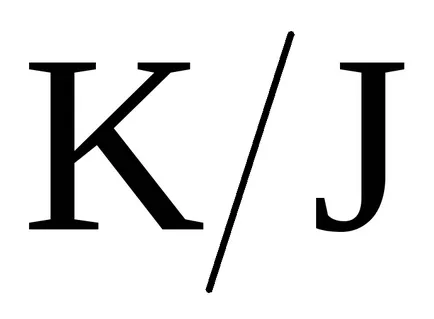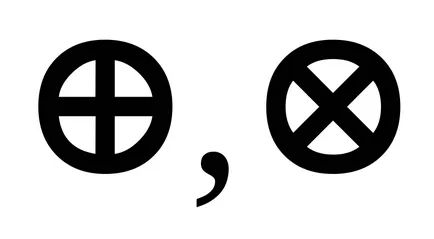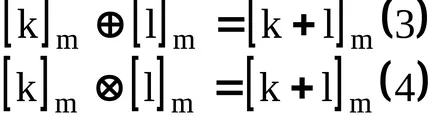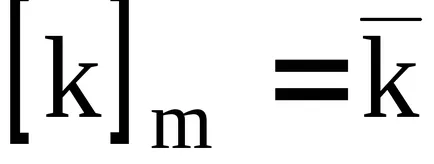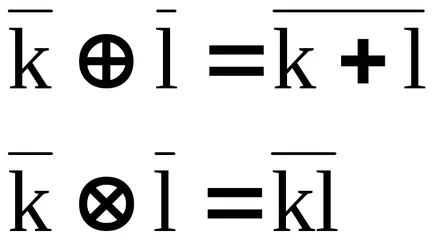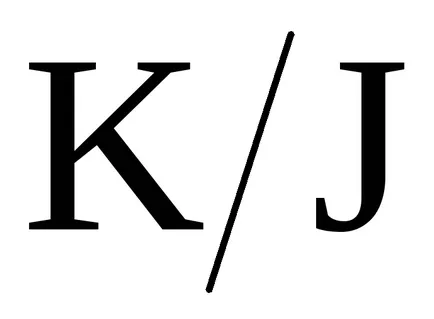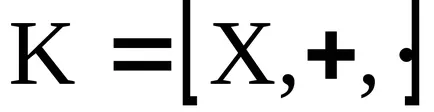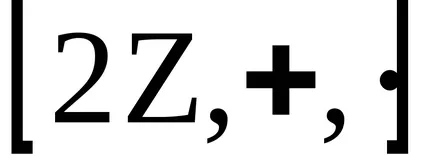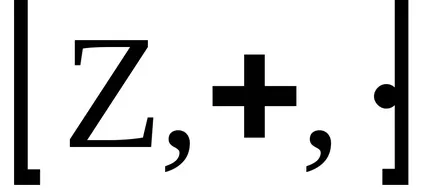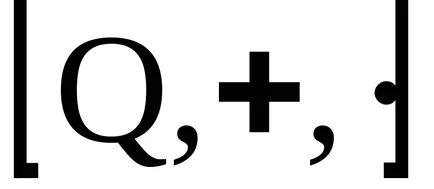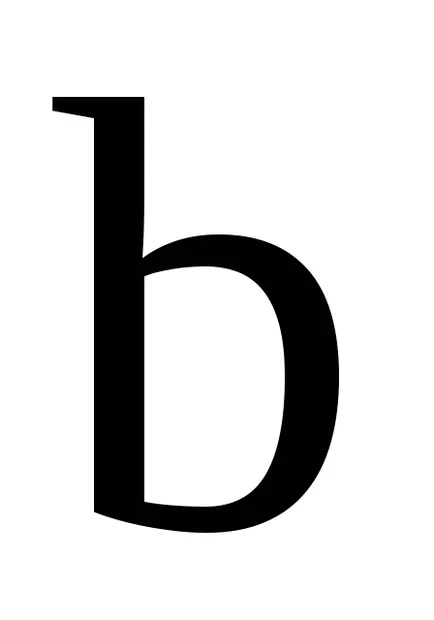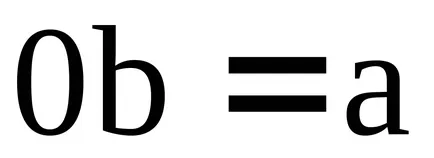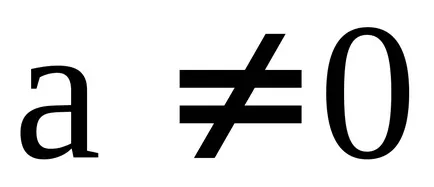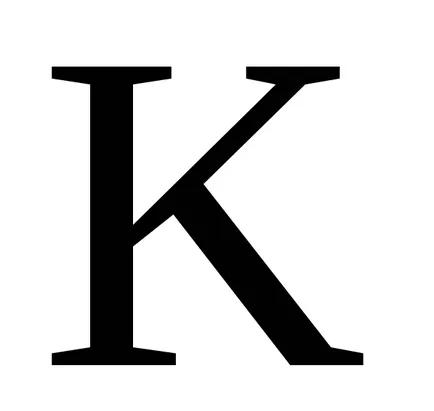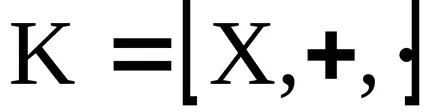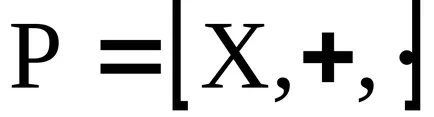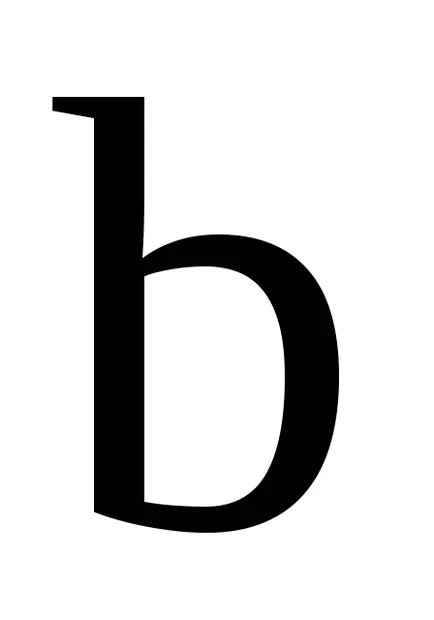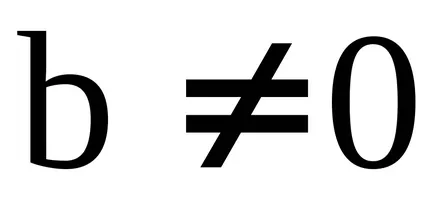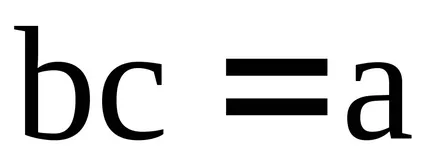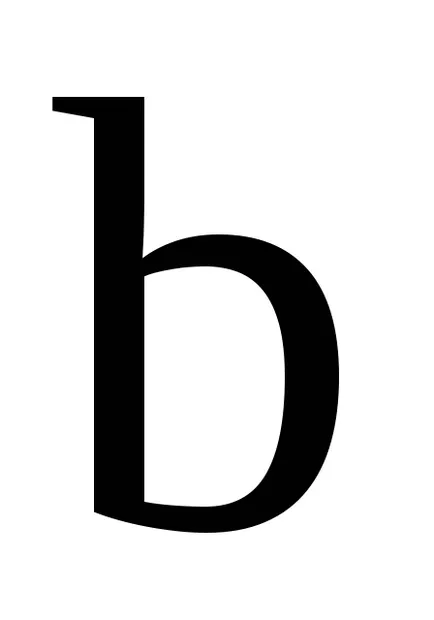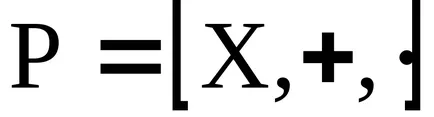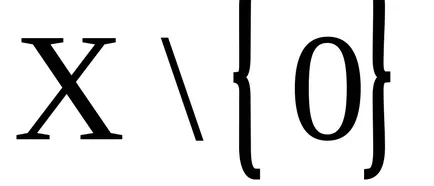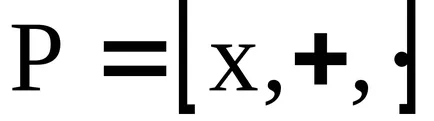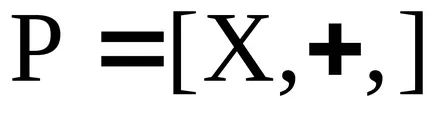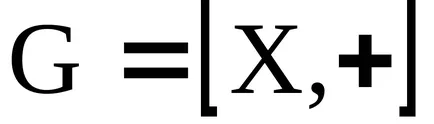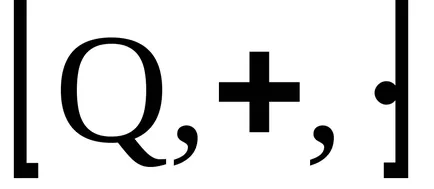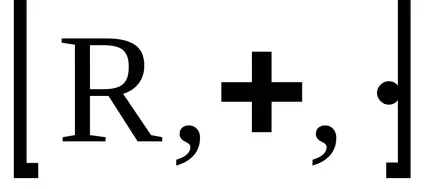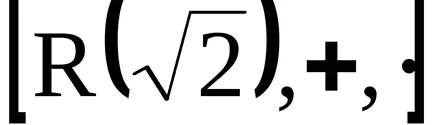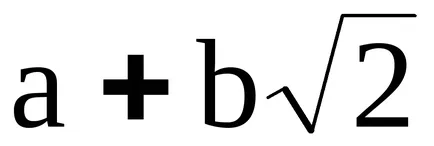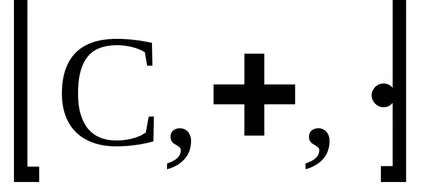Концепцията на идеала
пръстени
Н, подобен на този на нормалната делител групата G. Тази конструкция позволява да се доближава до коефициент пръстена
по същия начин, както в изграждането на фактор група G / Н.
нека
- идеални
.
Тъй като базовата пръстена
Това е добавка абелева група
, като елементи коефициент пръстени могат да изберат cosets
, където
, който nazyvayutsyaklassami остатъци модул идеален пръстен.
Теорема. Множество добавка cosets
форма фактор пръстен
с операции:
В допълнение, естествено карта vidayavlyaetsyaepimorfizmom (
- surjective).
Доказателство. Групата Abelian
всяка подгрупа
нормално, защото Затова, експресията (1) определя абелева група коефициент пръстен и картографирането е върху адитивни абелева група G и
.
Остава да се провери, че експресията (2) определя еднозначно размножаването на набор от добавки cosets
, т.е. Тя не зависи от избора на представителите на класовете.
нека
,
- представители на двете cosets
и
, т.е.
,
,
Остава да се покаже, че
.
В действителност, тъй
и
- идеални в K, а след това,
следователно
Те са в една и съща съседен клас с елементи
, което означава, че продуктът (2) е вярно.
Пример. Помислете за пръстена на целите числа
. В идеалния случай, че пръстенът
, т.е. набор от числа, кратни на m без следа.
Добавка съседен пръстен К клас идеален
Той има формата къде.
Множество cosets добавка съдържа точно
класове остатъчни модул
, и те имат следния вид:
Така, пръстенни елементи на фактор на
са класовете остатъчни модул
.
операции
, на koltsezadayutsya на фактор на класове на остатъчни вещества, както в миналото:
,
За да фиксира т, по-горе, за използване стенографски
:
Концепцията на пръстен-фактор
от идеалния пръстен
Тя ви позволява да създадете основни теорема на homomorphism на пръстени.
Определението на поле, протозои свойства.
Във всеки пръстен
изваждане се осъществява - обратната операция на добавяне:
От изпълнението на операциите дивизия - обратната операция за размножаване в определението на ринга не казва нищо. Тя може да се докаже, че по отношение на операция деление различни пръстени притежават различни свойства. Например, в пръстена четни числа
се раздели един номер от друг се извършва само в изключителни случаи; в този пръстен не е елемент, който ще споделя всички негови елементи.
В пръстена от числа
разделяне на един брой от друг се осъществява в изключителни случаи, но всички елементи на пръстена разделени от един и -1. В rationals на пръстена
операция деление винаги се извършва с изключение на деление на нула.
Забележка. Участък от нула е невъзможно във всеки пръстен: разделяне елемент
0 - означава да се намери елемент в пръстена
, че
, но когато
това не е възможно, тъй като за всеки елемент на ринга
:.
Колкото по-висока алгебра и по-специално в областта на математиката като цяло, играе специална роля комутативен пръстени. Тя се осъществява в които операция деление от деление на нула. Те са наречени полета.
Ние даваме няколко дефиниции на областта, които отразяват основните му характеристики.
Opredelenie1. комутативен пръстен
nazyvaetsyapolem и означен
, ако съдържа поне един елемент, различен от нула, и ако се извършва операция деление от делене на нула, т.е. за всички нейни компоненти
и
, от които
, тя съдържа един и само един такъв елемент
, че
:
елемент
Той призова частните елементи
и
и е писано като дроб.
Opredelenie2. Paul
е комутативен пръстен, в който nonzeros
образуват група в рамките на операцията на умножение:
мултипликативна група на полето.
Opredelenie3. поле
- комутативен пръстен с единство не е равно на нула, където всеки ненулев елемент е обратимо:
Както може да се види от определенията, област
Това е хибрид от двете групи - добавка абелева група
и мултипликативна свързани разпределителни право (сега един, на commutativity).
Забележка. Изискванията, включени в дефиницията на полето се наричат аксиоми област.
Определение. Полеви елементи са числа, наречени числови полета.
1. Пръстенът на рационални числа
Това е област.
2. Пръстенът на реалните числа
Това също е област.
3. Ring
номера на формата
, където
, Това е област.
4. Пръстенът на комплексни числа
Това е област.
Всички примери са числови полета. Примери за цифрови полета са обсъдени по-долу.