Как да се разделят една малка част от една малка част - 28 Януари, 2018
Разделете една малка част от една малка част не е толкова трудно, колкото изглежда. За да се разделят един от друг фракция, размените на числителя и знаменателя на втората част, а по-скоро разделение знак напишете знака за умножение. Така че сега трябва да умножите двете фракции.
- 1 Обратните числител и знаменател от втората фракция (фракция обратната). Числителя - номер на върха и в знаменателя - броят на дъното. Инверсия на фракцията - е намирането му обратна стойност. Така например, имат за задача: 2/3 ÷ 3/7. Включете втората част (3/7) и ще получите една малка част 7/3.
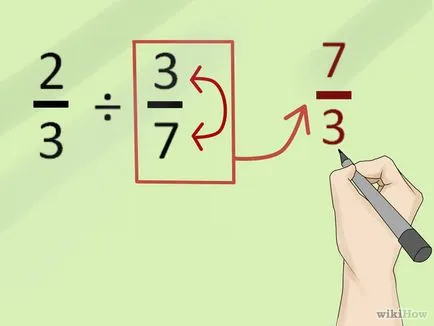
- Препишете проблема като 2/3 * 7/3.
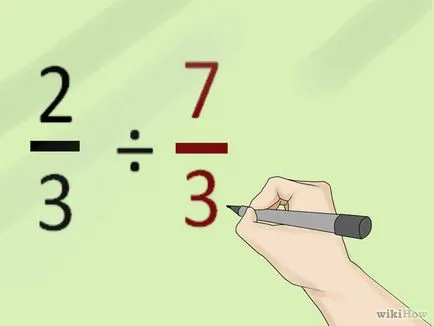
- Препишете проблема като 2/3 * 7/3.
- 2 Обърнете внимание на промяната в дивизия от знак за умножение знак (2/3 * 7/3). Това е вярно, тъй като разделянето на няколко равна на умножение по реципрочната на този номер.

- Помислете например за проблема 1 * 1/2. Нейното решение: 1/2. Ако пренапише проблема като 1 ÷ 2/1 (където 2/1 е обратното на 1/2), ще получите един и същ отговор: 1/2.
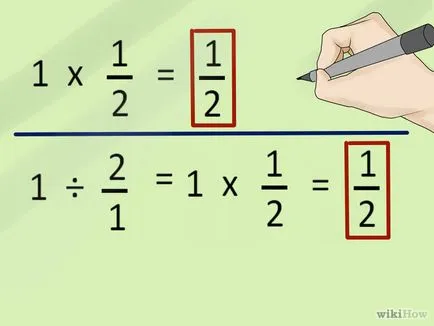
- Помислете например за проблема 1 * 1/2. Нейното решение: 1/2. Ако пренапише проблема като 1 ÷ 2/1 (където 2/1 е обратното на 1/2), ще получите един и същ отговор: 1/2.
- 3 Опростяване на двете фракции. За тази цел, се разделят на числителя и знаменателя на всяка фракция най-ниското си общ делител (GCD е най-голям брой, която разделя равномерно както на числителя и знаменателя на фракция). В нашия пример (2/3 х 7/3) или една от фракциите не е опростено.

- Пример (1) опростяване на фракции. Предвид задачата на 2/4 * 4/8. 2.4-1.2 може да се опрости (чрез разделяне както на числителя и знаменателя на тази фракция GBR = 2) може да бъде опростено и 4/8 до 1/2 (чрез разделяне както на числителя и знаменателя на тази фракция GBR = 4). Следователно, проблемът може да бъде пренаписана, както следва: 1/2 * 1/2.

- Пример (2) опростяване фракции. Предвид задачата на 4/3 * 9/2. Този проблем може да бъде пренаписана, както следва: 4/2 * 9/3 (когато се размножава фракции могат да бъдат разменени техните числители и знаменатели). След това, прилагането на по-горе метод, за да се опрости фракции пренаписване проблем във формата: 2/1 * 3/1.
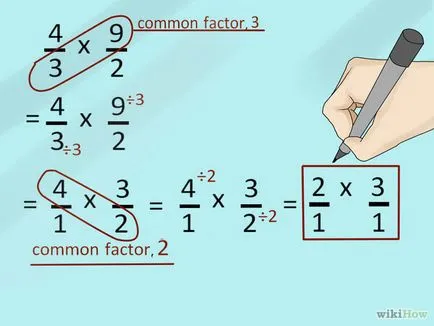
- Пример (1) опростяване на фракции. Предвид задачата на 2/4 * 4/8. 2.4-1.2 може да се опрости (чрез разделяне както на числителя и знаменателя на тази фракция GBR = 2) може да бъде опростено и 4/8 до 1/2 (чрез разделяне както на числителя и знаменателя на тази фракция GBR = 4). Следователно, проблемът може да бъде пренаписана, както следва: 1/2 * 1/2.
- 4 Умножаване фракции. За да направите това, умножете си номератори и след това се размножават си знаменатели. Ето как:
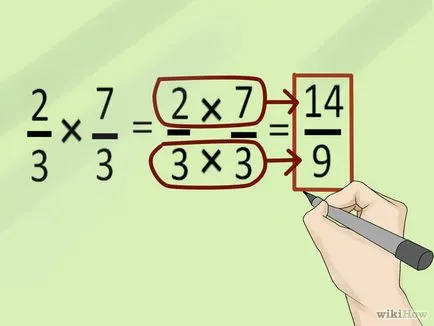
- Умножете числителите. В този пример, 2 х 7 = 14.
- Умножете знаменателите. В нашия пример: 3 * 3 = 9.
- Запишете получената фракция: 14/9.
- 5 Конвертиране грешен фракция в смесена номер (ако е необходимо). 14/9 - е неадекватно фракция като му числител над знаменател. Ако учителят изисква отговор под формата на смесено число, конвертирате в грешната фракция. Ето как да го направите:
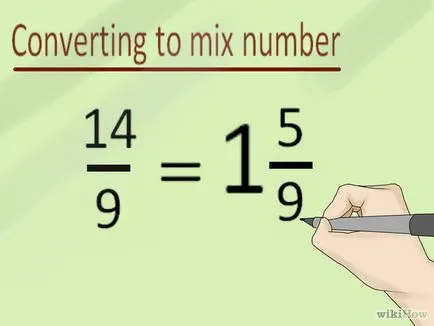
- Разделете числителя от знаменател (с остатък). В този пример: 1 = 14/9 (ost.5).

- Запишете в резултат на разделяне (1), като цялата част на смесени форми. По този начин, цялата част от смесен брой равна на 1.
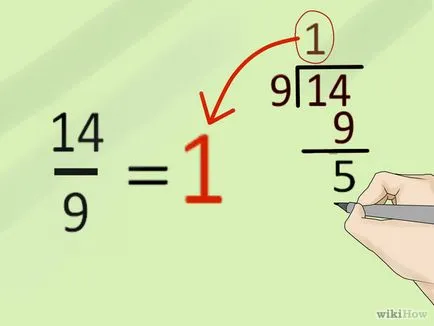
- В нашия пример, остатъкът е 5.
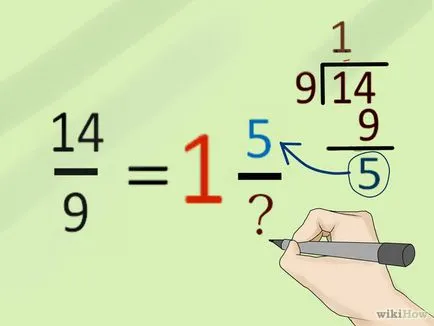
- Запишете остатъка (5) в числителя на дробна част от смесения броя и знаменателят на дробна част от неадекватно фракция смесен запис знаменател (9). По този начин, дробна част от смесения брой е 5/9.
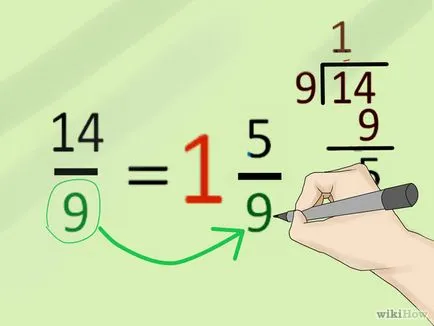
- Така че имаш смесена номер 1 5/9 (т.е. 14/9 = 1 5/9).
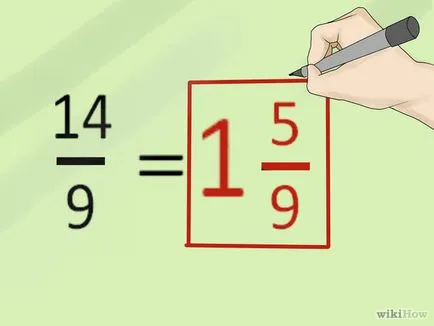
- Разделете числителя от знаменател (с остатък). В този пример: 1 = 14/9 (ost.5).
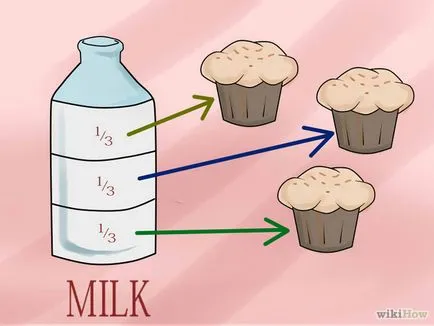
- 6 Илюстрация на пример за реалния живот на разделение алгоритъм. Например, вземете рецептата (това е един чудесен начин за консолидиране на живот или да го научи на друго лице). Например, рецептата за получаване на торти каза, че един счита торта 1/3 литър мляко. Трябва да разбера колко торти могат да бъдат направени от 1 литър мляко. Отговор - Три торти, и ето защо.

- 1 ÷ 1/3 = 3.
- Този израз може да се изписва като: 1 * 3/1 или 1 ÷ 1/3 = 3/1 = 1 * 3.
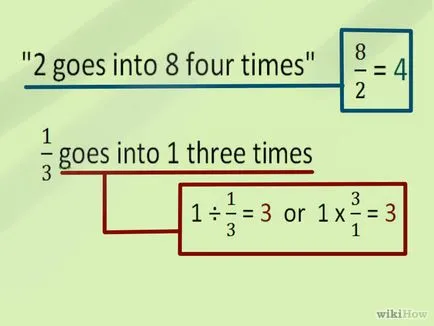
- 1 ÷ 1/3 = 3.
- Вашият учител може да ти го обясня по друг начин на разделяне на фракция от една малка, но най-често срещаната (и лесен) начин за разделяне.
- Внимателно прочетете изискванията на задачата. Ако те казаха да опрости една малка част, да го направи. Ако изискванията не са ясни, помолете ги учител.
- Когато се умножи фракции могат да бъдат опростени, без да променя местата на техните числители и знаменатели. Например: 1/4 * 2/1 = 1/2 * 1/1 = 1/2 (т.е. разделяне на знаменател (4) на първата фракция и числителя на (2) втора фракция 2).