Как да се чете матрицата
Понятието "матрица" е известен в линейната алгебра. Преди описанието допустимите операции на матрици, е необходимо да се въведат своето определение. Матрицата е правоъгълна маса от числа, съдържащи редица m редове и п броя колони. Ако т = п, след това матрицата се нарича квадрат. Матрици обикновено са отбелязани с главни букви като А или А = (Aij), където (Aij) - матрица елемент, и - брой линия, J - индекс колона. Като се има предвид две матрици А = (Aij) и В = (BIJ) със същия размер m * п.

инструкция
Сума матрица А = (Aij) и В = (BIJ) е матрица C = (CIJ) от същия размер. където неговите елементи са определени от CIJ CIJ = Aij + BIJ (I = 1, 2, ..., т- J = 1, 2, ..., N).
Присъединителните матрици има следните свойства:
1. А + В = B + A
2. (А + В) + C = A + (В + С)
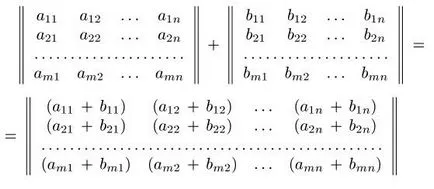
Продуктът от матрица А = (Aij) към реално число. Това е матрица C = (CIJ), където неговите елементи са определени от CIJ CIJ =. * Aij (I = 1, 2, ..., т- J = 1, 2, ..., N).
Умножение на броя на матрицата има следните свойства:
1. (??) А =? (A). и. - реални числа,
2. (А + В) =? A +? Б. - действителният брой,
3. (? +?) = B? B +? Б. и. - реални числа.
Въвеждане на умножение на матрици чрез скаларно, можете да въведете операция матрица от изваждане. Разлика матрици А и В е С матрица, която може да се изчисли според правилото:
С = А + (-1) * B
Matrix продукт. Матрица може да бъде умножена по матрица В, когато броя на колоните на матрицата А е броя на редовете на матрицата В.
Продуктът от матрица А = (Aij) на измерение m * п в матрица B = (BIJ) на измерение п * р е матрицата С = (CIJ) на измерение m * р, където елементите CIJ се определя от формула CIJ = AI1 * B1J + AI2 * b2j + ... + Ен * BNJ (I = 1, 2, ..., т- J = 1, 2, ..., п).
Фигурата показва пример на продукт с матрици на измерение 2 * 2.
Матрицата продукт притежава следните свойства:
1. (А * В) * C = A * (B * C)
2. (А + В) * C = A * C + B * С или A * (В + С) = A * B + A * C
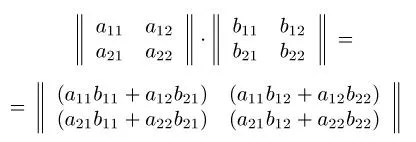
Съвет 2: Как да се изчисли обратната матрица
Матрицата се счита за обратна на матрицата, ако те образуват умножаване единица матрица Е. Терминът "обратен матрица" съществува само за квадратна матрица, т.е. Matrix "две по две", "три на три", и т.н. Обратното матрица е обозначен с горен "-1".

инструкция
За да се намери обратна на матрица, се използва формулата:
А ^ (- 1) = 1 / | А | Х ^ т, където
| A | - детерминантата на А,
А ^ т - на транспонирана матрица на кофактори на съответните елементи на матрицата А.
Преди да се пристъпи към определянето на инверсната матрица, се изчислява детерминанта. Matrix "две по две" детерминанта се изчислява, както следва: | A | = A11a22-a12a21. В детерминанта на всяка квадратна матрица може да се определи с формулата: | А | = (- 1) * (1 + й) X X A1J Mj където Mj - допълнително Мала да A1J елемент. Например, матрицата "две по две" с елементи на първия ред a11 = 1, А12 = 2 за втория ред 3 = А21, А22 = 4 ще бъде равна на | А | = 1h4-2h3 = -2. Имайте предвид, че ако дадена матрица детерминантата е нула, обратната матрица за него съществува.
След това намерете матрица от непълнолетни. За тази психически зачеркнете колона и ред, при който елементът в процес на разглеждане. Останалите номера ще бъде непълнолетния на елемента, тя трябва да бъде написана на матрица от непълнолетни. В този пример, за незначително елемент a11 = 1 е M11 = 4 = A12 с 2 - 3 = M12 за a21 = 2 - 3 = M21 за А22 = 4 - M22 = 1.
На следващо място, намери матрицата на кофактори. За тази цел промяна на знак и елементите са диагонално: и а12 и 21. По този начин, елементите на матрицата са равни на: 4 = A11 и А12 = -3, -2 = А21, А22 = 1.
След намиране на транспониране матрица на кофактори на А ^ т. За тази матрица кофактори линия запис в колоните на транспонирана матрица. В този пример, матрица транспониране ще има следните елементи: 4 = A11 и А12 = -2, -3 = А21, А22 = 1.
Заменете стойностите, получени в оригиналната формула. инверсна матрица А В * (- 1) е равна на произведението на -1/2 = 4 елементи a11, А12 = -2, -3 = А21, А22 = 1. С други думи, обратни матрични елементи са равни на: a11 = -2, a12 = 1, a21 = 1.5 А22 = -0.5.