Как да намерите областта на кръг, квадрат, триъгълник
Как да намерите областта на кръг?
Обиколка - затворен равнина крива на всяка точка, която е на еднакво разстояние от дадена точка (център) лежи в същата равнина, като кривата.
Кръгът - част от равнина, ограничена от окръжност.
Радиус - отсечка, която свързва центъра на кръга с точка от нея, както и продължителността на този сегмент. Обикновено oboznachaetsyaR.
Диаметър - отсечка, свързваща двойка най-отдалечени един от друг по периферията на точки, а дължината на този интервал. Диаметър винаги минава през центъра на кръга. Обикновено oboznachaetsyaD Ильо. Диаметър, равен на два пъти радиуса на кръга: D = 2R, R = D / 2.
Съотношението на дължината на окръжността към нейния диаметър е един и същ за всички перифериите. Тази връзка е трансцендентно число, което се означава с гръцката буква пи: π = 3,14159.

Как да намерите областта на триъгълник?
Триъгълник - плосък геометрична фигура, ограничена от три дължини на двойки пресичащи се линии. Точките на пресичане nazyvayutsyavershinami treugolinika и обикновено определени от капиталови латинските букви: А, В, С Velichinyuglov във върховете на които се пресичат съответните линии обикновено са обозначени с гръцки букви: α, β, у. срещуположни ъгли линия сегменти очертаващ триъгълник nazyvayutsyarebrami (страни) на триъгълник и са означени съответно А, В, С.
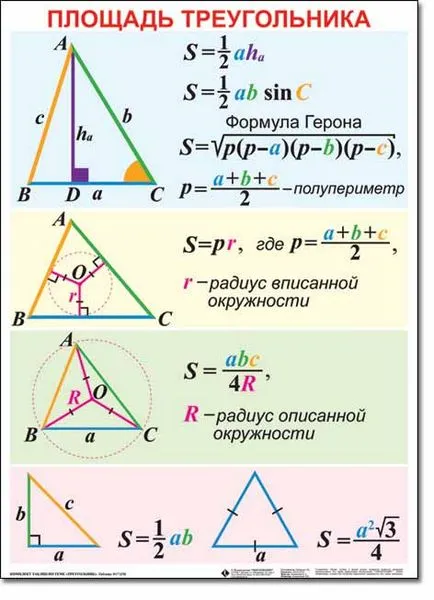
Показани са формули, чрез която може да се намери в областта S на триъгълника с върхове A, B, C, съответните стойности на ъглите а, β, γ и противоположните страни на тях, Ь, с:
S = а · б · грях (γ) / 2 = а · в · грях (β) / 2 = б · в · грях (α) / 2,
S = 2 · грях (β) · грях (γ) / (2 · грях (β + γ),
S = √ (р · (р - а) · (р - б) · (р - с)) (херонова формула) където √ (.) - определянето на корен квадратен, р = (A + B + C) / 2 - semiperimeter триъгълник.
S = а · ха / 2 = б · Hb / 2 = C · HC / 2. където ха - височина понижава от връх А към страна на, зб - от върха B към страничната б, HC - от връх С до страничната в.
S = R · стр. където R - радиус на вписаната, р = (A + B + C) / 2 - половината периметър на триъгълника.
S = а · б · в / 4R, където R - радиус на окръжността, описана около триъгълника.
(. X3 Y3) Ако декартови координати са определени точки в равнината А (. X1 y1), В (. X2 y2) и С, зона S може да се намери чрез следното уравнение (детерминанта чрез втори матрици ред за координиране разлики):
S = | (х1 - 3 пъти) · (y2 - Y 3) - (х2 - 3 пъти) · (y1 - Y3) | / 2. където |. | - определяне на модула. Тази формула е получен от експресията на вектора продукта от двата вектора в равнина, която е в величина равна на детерминанта на техните координати.
Как да намерите областта на правоъгълен триъгълник?
Тя се нарича правоъгълен триъгълник. един ъгъл, който се намира на 90 ° (по-вдясно). Тъй като сумата от ъглите на триъгълник е 180 °, под прав ъгъл на триъгълника може да бъде само един.
Показани са формули за изчисляване формула S. spetsificheskikie зоната за правоъгълни триъгълници. Легенда: а - дължина на хипотенузата (противоположната страна на десния ъгъл), а. б - дължина на краката (страни, съседни на прав ъгъл), алфа. β - тези количества катет противоположни ъгли (α + β = 90 °).
За две катет: S = а · б / 2
Чрез катет и хипотенузата: S = а · SQRT (С2 - 2) / 2 = б · SQRT (С2 - б 2) / 2.
където SQRT (.) - определянето на корен квадратен
КАК да намерите площта на квадрат?
Square (от латинската Квадрат -. Четириъгълна) - десен квадрат, на която всички страни и ъгли са равни. Може да се определи като правоъгълник, в която две съседни страни са равни помежду си, или като ромб, в който всички ъгли са прави ъгли.
Симетрия. На площада има най-високата симетрия между всички четириъгълници. Той разполага с:
- Четири двукратни симетрия ос (равнина фигура, което е еквивалентно отражения), две от които се простират по протежение на диагоналите на квадрат, а другите две - паралелни страни;
- четвърта ос на симетрия (минаваща през центъра на квадрат, перпендикулярна на неговата повърхност).
Диагонал. На площада има две диагонали свързващи несъседни върхове. Диагонал на площада са ъглополовящи на неговите ъгли се пресичат в центъра на площада под прав ъгъл една към друга и се делят на две. Всеки диагонал разделя квадрата на две равнобедрен правоъгълен триъгълник. Две диагонали заедно разделят на площада в четири равнобедрен правоъгълен триъгълник.
Ако означим страната на квадрат. дължината на диагонала D се изчислява съгласно Питагоровата теорема:
Вписан и окръжности. Вписан в квадрат кръг е допирателна към центъра на квадрата от всички страни и има радиус R. равно на половината от страна на квадрат. Описан квадрат около обиколката преминава през всички негови върхове и има радиус R., равна на половината от дължината на диагонала на квадрат г:
Периметър и област. Периметър P квадратен сума от дължините на четирите страни. Районът S е равна на квадрата на квадрата на дължината на страните му:
P = 4а = 8R = 2√2 · R,
S = 2 = 4R 2 = 2R 2.
Как да намерите областта на трапец?
Акробатика - четириъгълник в които две успоредни страни (база на трапеца), а останалите - неуспоредни (страничните страни на трапеца). Сегмент свързваща средата на двете страни, се нарича средна линия на трапеца.