Изследване, социална мрежа
функция консумация Целева е дадено. Цена е първата полза, а втората полза. Доход е D = 550. търсене:
а) безразличие криви;
б) най-добрият набор от ползи.
1) безразличие криви са от вида:
Ние получаване на множество хиперболи координатна намира в първото тримесечие и се намира на различни разстояния от произхода, в зависимост от стойността на константа В.
2) Да се намери оптимално набор от ползи. оптимално програмиране проблем има следния вид:
.
За решаване на проблема на бюджетно ограничение изразя една променлива върху друго :.
Заместник целевата функция :.
Ние считаме, производно и се равняват на 0:
По този начин, оптимално всички предимства е 55/3 и 55/2 единици.
Налице е баланс на два взаимосвързани сектори (селско стопанство и инженерни) за предходната година.
Намери крайния продукт на всеки сектор, нетна мощност на всеки отрасъл, коефициентите на матрицата на преките разходи. Каква ще бъде общата продукт на всеки сектор, ако крайният продукт на селското стопанство трябва да се увеличи с 40%, и инженеринг за намаляване с 20%. Матричен материал междубраншови връзки Xij и матрица брутната продукция Xj са дадени в таблицата.
, .
Крайният продукт се определя по формулата:
,
при което - матрицата за самоличност, - преките разходи матрица, чиито елементи са определени от това правило.
.
- крайните индустрии продукта.
Нека да нетните производствени отрасли, като се използва формулата:
.
Ние имаме - чисто производство в / х,
- чисто технически изделия.
За общия продукт, съответстващ на новата форма на крайния продукт, се използва формулата:
.
Ние намираме обратната матрица:
.
Браншова производство и разпространение на баланса на 4 сектора е както следва:
Намери крайния продукт на всеки сектор, нетна мощност на всеки отрасъл, коефициентите на матрицата на преките разходи. Какъв ще бъде крайният продукт на всеки сектор, ако брутният продукт на първия индустрия ще се увеличи с 2 пъти през втората половина ще се увеличи, трета няма да се промени в четвърти - ще намалее с 10%.
Матрицата на междубраншови отношения материал Xij и матрица на брутната продукция Xj са изброени в таблицата по-долу:
1) Виж нетните производствени индустрии, като се използва формулата:
.
,
,
,
.
2) крайните отрасли на продукта:
.
,
,
,
.
3) Елементите на преки разходи се определят от правилото.
4) Новият БВП.
крайните сектори на продукта:
.
,
,
,
.
За тази функция на производството, за да се намери средната и пределната производителност на всеки ресурс, лично еластичността на изход за всеки ресурс, гъвкавостта на производството и пределната норма на заместване технология.
, .
Пределната производителност, са:
, .
Лично еластичност са:
,.
правило технологично заместване е :.
Една компания прекарва a1 = 7 хил. Тона на ресурси и b1 = 32 хил. Часове на труд за производството на C1 = 65000. Единици. Разширяването на производството бе установено, че най-a2 цена = 8-ми. Освобождаване Тонове ресурс се увеличи до С2 = 67000. Единици за сметка на увеличаване на сложността на б-2 = 34000. Часове, освобождаване се увеличили до С3 = 70000. Units продукти. Намери линейна функция на производството и производствена функция на Коб-Дъглас.
Пишем за удобство на суровите данни в табличен вид:
За да намерите б използва първата колона на таблицата:
В резултат на това производството функцията линеен е от вида:
.
Функцията за производство на Cobb-Дъглас е както следва:
.
, .
За да намерите б използва първата колона на таблицата:
В резултат на това производството функция на Cobb-Дъглас е както следва:
.
БСК се състои от 4 предприятия (п = 4). Общата капиталова инвестиция е 700 млн. Разтрийте. (В = 700), сумата, разпределена на кратни предприятие на 100 млн. Rub. Ако й-то компанията получава инвестиция от х млн. Разтрийте. увеличението на годишна печалба в този бизнес ще бъде FJ (х) млн. търкайте. годишно. Стойности на функции FJ (х) са дадени в таблицата по-долу:
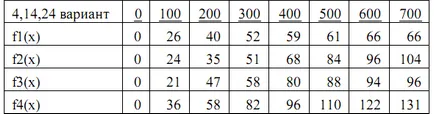
Задължително да се намери разпределението на инвестициите между предприятия, която да е максимално общия ръст на печалбата във всички предприятия заедно.
Съставляващи първата спомагателни таблица: