Изграждане на истината маси
Приоритет в изпълнението на операциите на реда са скобите.
Алгоритъм за построяване на функция за истина маса логика
Определяне на броя на редовете: Брой редове = $ 2 ^ N + 1 $ (глава линия). $ N $ - брой прости изрази. Например, там е $ 2 ^ 2 = 4 $ комбинация определя стойности на променливите за функциите на три променливи за функциите на две променливи - $ 2 ^ 3 = 8 $ т.н.
Определяне на броя на колоните: Брой Колони = брой променливи + брой логически операции. При определяне на броя на логическите операции също се вземат под внимание на реда на тяхното изпълнение.
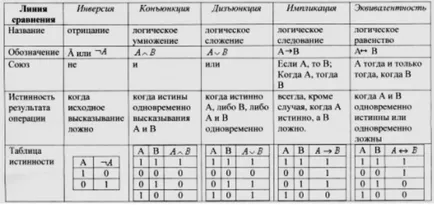
Напълнени колони представят логически операции резултати в последователност дадена истина маса на основните логически операции.
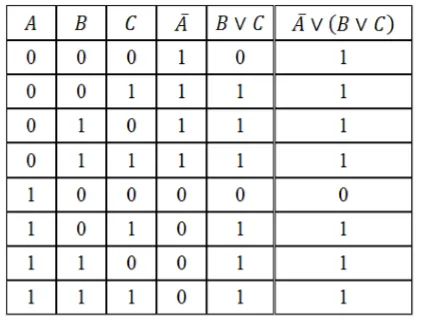
Създайте таблица на логическия израз е вярно $ D = \ бар \ вее (B \ вее C) $.
Определяне на броя на редовете:
Брой на общи изрази - $ п = 3 $, а след това
брой редове = $ 2 ^ 3 + 1 = 9 $.
Ние определяме броя на колоните:
Броят на променливи - $ 3 $.
Броят на логически операции и тяхната последователност:
- Инверсия ($ \ бар $);
- дизюнкция, защото тя е в скоби ($ B \ вее C $);
дизюнкция ($ \ Номера \ VEE \ наляво (B \ VEE С \ дясно) $) - желания логически израз.
Брой колони = $ 3 + 3 = 6 $.
Попълнете таблицата, дадена в таблицата истината на логически операции.
Определяне на броя на редовете:
Брой на общи изрази - $ п = 3 $, а след това
брой редове = $ 2 ^ 3 + 1 = 9 $.
Ние определяме броя на колоните:
Броят на променливи - $ 3 $.
Броят на логически операции и тяхната секвенция:
- отричане ($ \ бар $);
- дизюнкция, защото тя е в скоби ($ A \ вее B $);
- съюзът на ($ (А \ VEE В) \ bigwedge \ Номера $);
- отричане, което ще означаваме $ F_1 $ ($ \ Номера> $);
- дизюнкция ($ A \ VEE С $);
- връзка ($ (А \ VEE С) \ bigwedge B $)
- отричане, което ще означаваме $ F_2 $ ($ \ Номера $);
Брой колони = 3 + $ 11 = $ 8.
Попълнете таблицата, дадена в таблицата истината на логически операции.
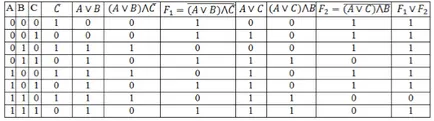
Алгоритъм за изграждане на логическата функция от нейната истина маса
- Разпределяне поредна истина маса със стойността на функцията равно на $ 1 $.
- Добави от желаната формула, както множество логическа дизюнкция на изразяване. Размерът на тези изрази е равен на броя на избрани редове.
- Всеки логически израз в тази дизюнкция написана като съчетание на аргументи на функция.
- В случаите, когато стойността на някои от аргументите на функцията в съответния ред от таблицата е зададен на $ 0 $, а след това този аргумент е написана под формата на неговото отрицание.
Решете контрол по всички предмети. 10 години опит! Цена от 100 рубли. период от 1 ден!