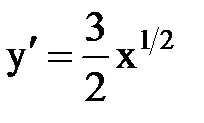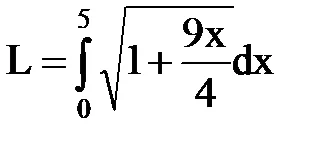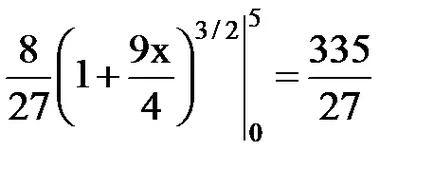Изчисляване дъга дължини равнина криви - studopediya
В елементарна геометрия измерва дължината на права линия сегменти, както и дължината и обиколката на неговите части. За дължината по периферията е взето в рамките на периметъра на окръжност вписан в правилен многоъгълник с неограничен увеличение на броя на техните страни. Ние се обобщи това понятие за всяка крива.
Определение. DlinoyL дъга AB е границата, към която периметъра на вписания полигонална в тази дъга, когато броят на неговите дялове без лимит, а максималната от дължините на връзките отива към нула:
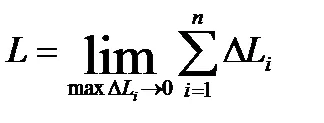
Криви, за които съществува тази граница, наречени преодолими.
Теорема. Нека krivayaAV дава с уравнението у = F (х), където е (х) - непрекъсната функция като непрекъснат производно във всички точки в сегмент [а, Ь]. Тогава дъга AB е с дължина:
,
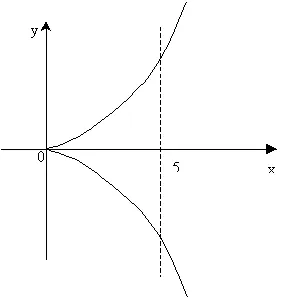
Пример 1.Nayti semicubical парабола дължината на дъгата от х = 0 до х = 5. Решение: Кривата е симетрична по отношение на оста х. Ние намираме дължината на горния клон на кривата. От уравнението намираме