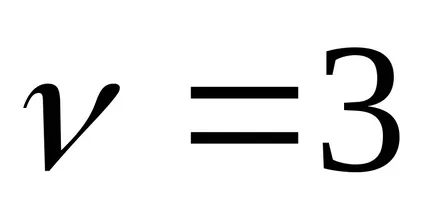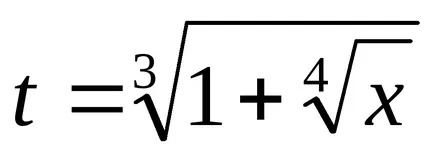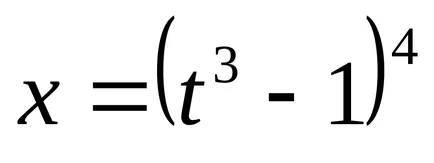Интеграция на двучленни диференциали

Примери. Нютонов нарича тип диференциал.

,

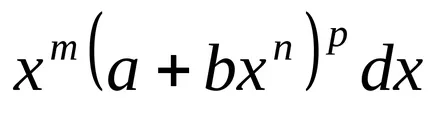
където а, Ь - всички параметри т, п, р - рационални числа. Нека да разберете случаите, когато тези изрази са интегрирани в краен вид.

Един такъв случай е пряко ясно, че ако р - цяло число (положително, нула или отрицателни), след това този израз е от типа проучен в предишното

. Това означава, че ако след означават най-малко общо кратно на знаменателите на фракциите и , това, което имаме тук е израз на формата , така че да е достатъчно, за да се рационализира заместване .

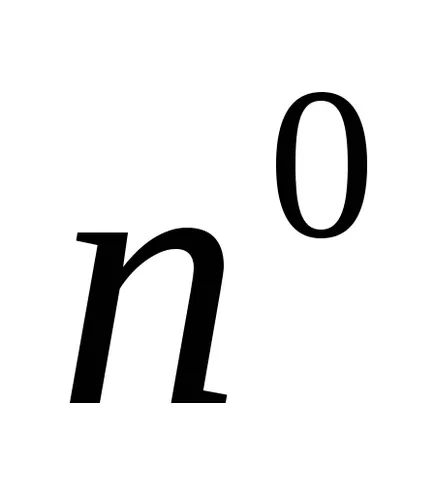
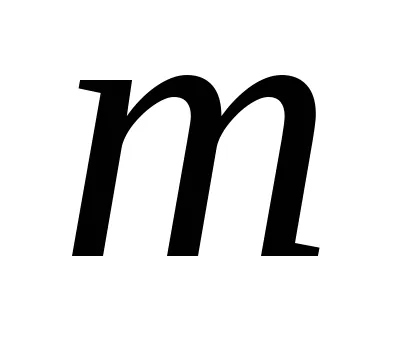
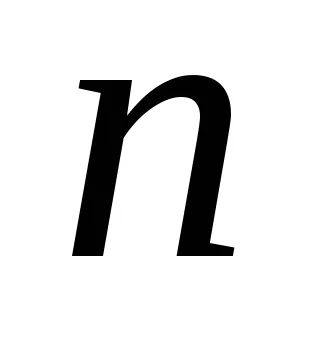
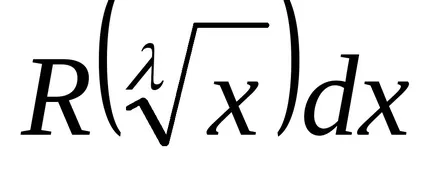
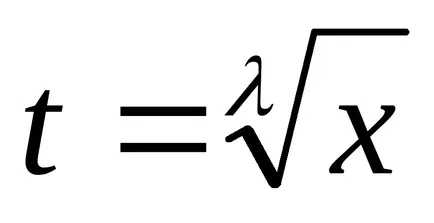
Сега ние се трансформира така чрез заместване

.

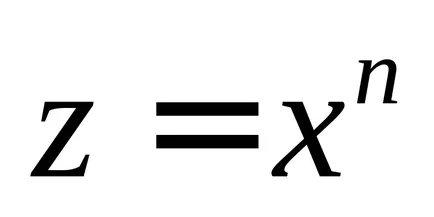
и пускане, за краткост

,

.

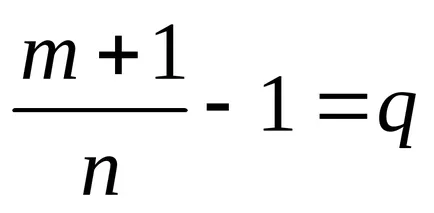
ако

- цяло число, ние отново се достигне до експресията на изследваната тип. Всъщност, ако ние означаваме знаменателя , преобразуваната експресията е . Рационализация на подинтегрален може да се постигне наведнъж - заместване

.

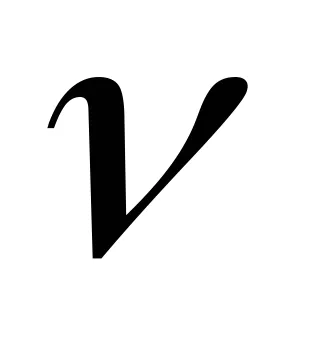
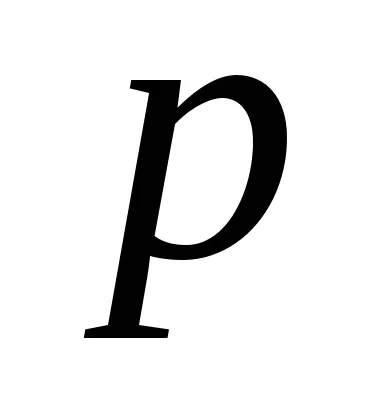
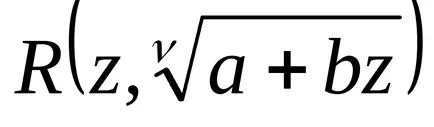
Накрая, втората съставна пренаписване (2), както следва:

.

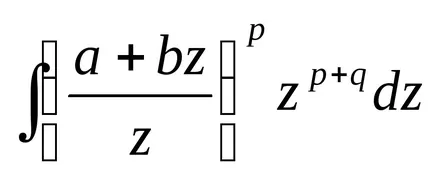
Лесно е да се види, че за

Като цяло, ние сме също учи случая: преобразуваната израз е . В подинтегрален в тази интегрална рационализира и веднага заместване

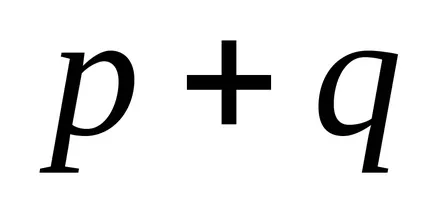
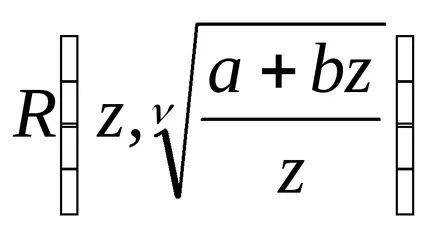
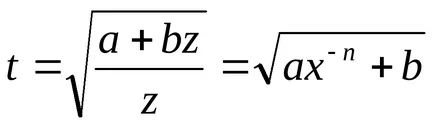
По този начин, както интеграл (2) може да се изрази в затворена форма, ако цялото е едно от числата

или (еквивалентно) едно от числата

.

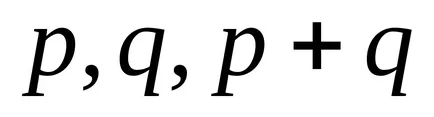
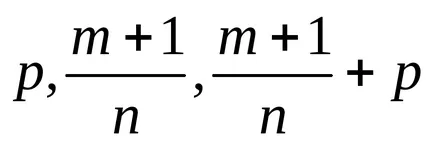
Тези интегрируеми случаи по същество, все още са били известни на Нютон. Въпреки това, само в средата на деветнадесети век, PL Chebyshev създаде забележителен факт е, че други случаи на integrability в крайните срокове за двучленни диференциали не.

1). тук

, ,; защото

,

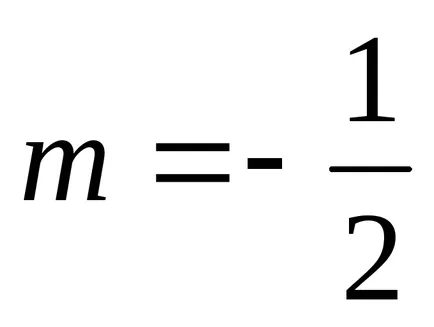
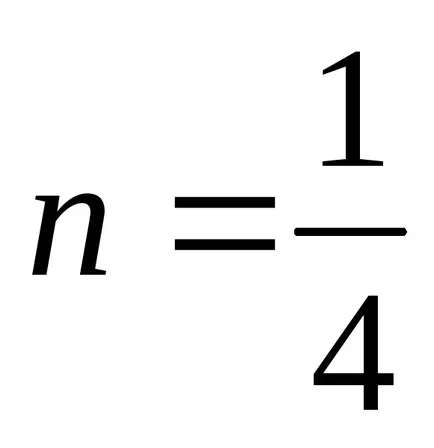
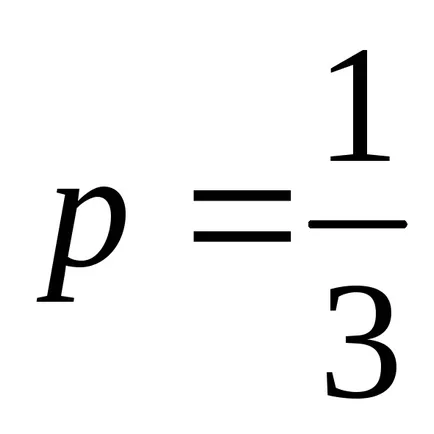
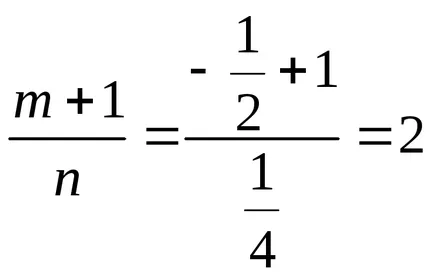
След това ние имаме втория случай на integrability. Забелязвайки, че

, поставени (по правило)

, , ;