хистограма

Наречен хистограма графика приравняване на плътността на случаен принцип разпределение на данни. При конструиране на хистограма на стойностите на случайна променлива област (а, б) е разделена на множество сегменти на контейнера, и след това изчислява процента на данни, включени във всеки сегмент. За хистограмите в Mathcad има няколко вградени функции.

Хистограма с произволни разделителни сегменти

- ист (междинно съединение, х) - вектор, на честотни данни, въведени интервалите хистограма;

- Int - вектор, чиито елементи определят сегменти хистограма във възходящ ред на

- х - вектор, на случаен данни.

Ако векторът е INT бен предмети, функцията резултат ист () има същия брой елементи. Хистограма показано на фиг. 9.12.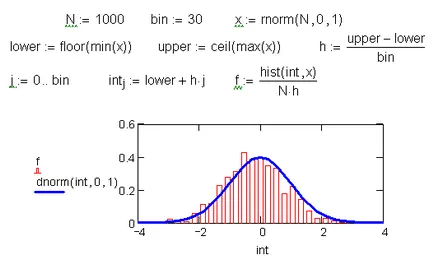

Фиг. 9.12. Хистограмата на нормалното разпределение на вероятностите.

Хистограмата е изградена за N = 1000 случайни числа записани под формата на вектор х. Намерени минимум (по-ниска) и максималните (горните) стойности на случайни числа и ги държи закръгляване до числа. След намерено почистване разделена на интервали бен Int вектор се състои от сегменти и адаптиран хистограма изчисление ист (). Векторът може да се настрои INT различни сегменти ширина.

Хистограмата с разделянето на равни сегменти

Ако не е необходимо да се определят различни ширина хистограма сегменти, че е по-удобно да се използва опростена функция ист един (). За тази цел функция хистограма ():

- хистограма (бен, х) - размер хистограма матрица binx2, състояща се от колона на преградни сегменти и честота колона проникване на данните;

- бен - броят на хистограма сегменти;

- х - вектор, на случаен данни.

Фиг. 9. 13 е пример хистограма () функции на употреба. Предимството му - лекотата на строителство и липсата на нормализиране:

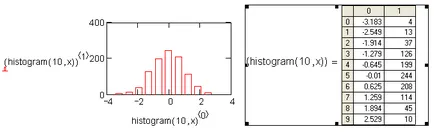
Фиг. 9.13. Фигура матрица хистограма.

Ето един пример. Задължително за определяне на числения диапазон (L, U), в която ще лежи с вероятност от 75% дисперсия на нормална случайна променлива въз основа на размера на извадката на броя N. Този проблем е решен в статистиката използване χ2 разпределение (Фигура 9.14.):

Фиг. 9.14. χ2 разпределение

Споменатият интервал се нарича (1-α)% доверителен интервал. При решаването на този проблем за изчисляване на стандартното отклонение се използва селективно функция СтОткл (). Статистиката често използвани изрази, които са по-удобно да се напише условията на функциите в тази нормализация, за тази цел, и те се появява в Mathcad'e.

Уреждане и графична референтна 1

- запознат с характеристиките на данни статистически население;

- запознаят с вградени функции за обработка на данни, статистически население;

- проучи процедурата по обработка на статистическата популация;

-получите някои статистически характеристики на масива от данни.

Задача. Създаване на статистическата съвкупност, с помощта на генератор на случайни числа от таблицата 9.1. Брой на статистическите цифри sovokupnostimprinyat собствени. Определяне на центъра на групиране статистическа популация (вж. Фигура 9.1), стойността на разсейване (вж. Фиг. 9.2). Построява хистограма с произволни преградни сегменти (вж. Ris.9.12) и хистограма разпределя на равни сегменти (вж. Фиг. 9.13).