Хипербола - крива
Образуването на геометрична, което се нарича хипербола, - плоска крива на втората цифра за състояща се от две криви, които са съставени от друг и не се припокриват. Математическата формула за описване е както следва: у = к / х, ако броят под индекс к не е равна на нула. С други думи, в горната част на кривата непрекъснато се стремим към нула, но никога няма да се пресече с него. От позицията на точката на изграждането на хипербола - сумата от точки в самолета. Всяка такава точка се характеризира с постоянно разстояние от модула на разликата на двете фокусни точки.
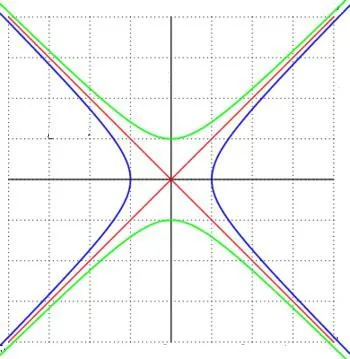
Плосък крива се разграничат основните функции, които са присъщи само за нея,
- Хипербола - това са две отделни линии, наречени клонове.
- В средата на голяма ос пъти е в центъра на фигурата.
- Върхът е наречен един до друг по отношение на двата клона.
- Фокусно разстояние е разстоянието от кривата на центъра на един от фокусите (означен "в" писмото).
- Много хипербола ос описва най-късото разстояние между клонове линии.
- Огнища лежат на главната ос, при условие, на същото разстояние от центъра на кривата. Линия, която поддържа основната ос, наречена напречната ос.
- Голяма полуос - е изчисленото разстояние от центъра на кривата на един от върховете (означени с буквата "а").
- Права линия, простираща се перпендикулярно на напречната ос през центъра му, наречена ос на конюгат.
- Координационно параметър определя интервала между фокуса и хиперболата която е перпендикулярна на напречната ос.
- Разстоянието между фокуса и асимптотата се нарича параметър влияние и обикновено е кодирана във формулите по буквата «б».
В конвенционален декартови известно уравнение от които конструкция може хипербола изглежда: (х 2/2) - (Y 2 / б 2) = 1. вида на крива, която има същата половин линия се нарича равностранен. В правоъгълна координатна система, е възможно да се опише просто уравнение: XY = на 2/2, с огнища на хиперболата трябва да се намира в точките на пресичане (а, а) и (-а, -а).
Всяко паралелно крива хипербола могат да съществуват. Това е нейната версия на химична връзка, в която осите са обърнати с асимптотата остане на земята. Оптичните свойства на формата е, че на един въображаем източник на светлина в центъра на вниманието на втората част е в състояние да се отрази и да попречи на втората фокуса. Всяка точка на потенциала на хиперболата има постоянна връзка с фокус на разстояние до всяко разстояние от направляващата. Типични плоска крива може да проявява както огледало и ротационна симетрия, когато се завърта на 180 ° в центъра.
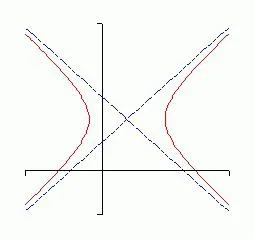
Изместването на хиперболата се определя цифров характеристика на конична част, което напречно сечение показва степента на отклонение от идеалното кръг. В математически формули, цифрата, посочена от буквата "е". Ексцентритет обикновено инвариантен по отношение на равнината на движение и процеса на приликата трансформации. Хипербола - цифра, в която ексцентричността винаги е равен на съотношението между фокусното разстояние и главната ос.
