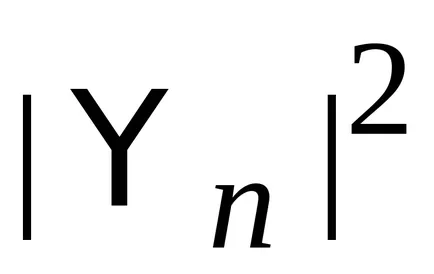Hermitian оператори
Реал физична величина, неговото измерение - определено. Тези условия за собствените стойности на Hermitian оператор предоставя. Операция Hermitian конюгиране се определя от неразделна квадратна форма. Тази форма описва, между другото, на средната стойност на измерваната величина.
Hermitian долепени
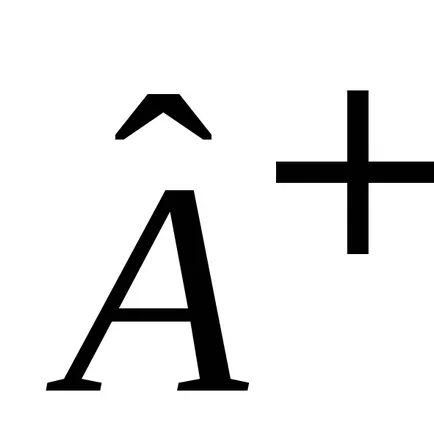
Интеграцията се извършва през целия обем на мястото, където може да има частица.
Свойства на Hermitian спрежение
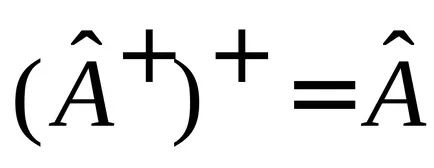
,
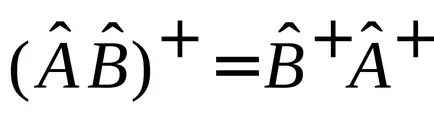
да се докаже,
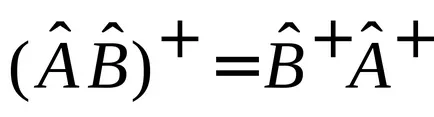
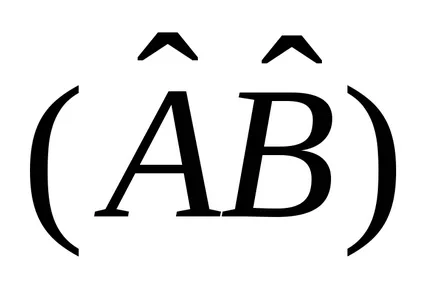
и последователно - първо на оператора

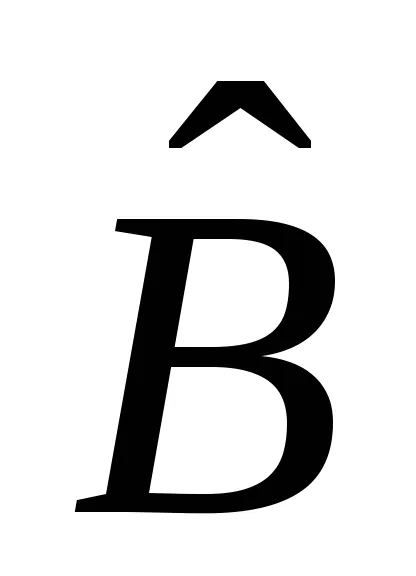
.
Сравнете от дясната страна на уравненията получени.
Останалите отношения се доказват.
Hermitian оператор не се променя, когато Hermitian спрягането
От (2.11) получаваме определението за Hermitian оператор
Следователно Hermitian оператора може да се премества в неразделна квадратна форма от една функция в друга.
Свойства на Hermitian оператор.
1) Собствените стойности са реални.
вярвам, където
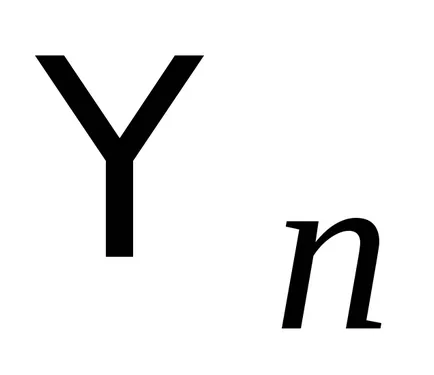

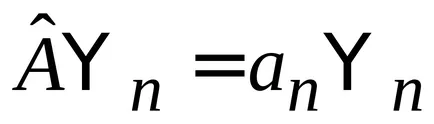
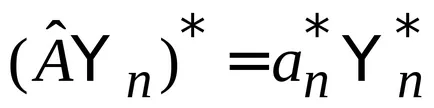
.
- измерената стойност е реална.
2) eigenfunctions, съответстващи на различните собствени стойности са ортогонални.
За собствените си функции
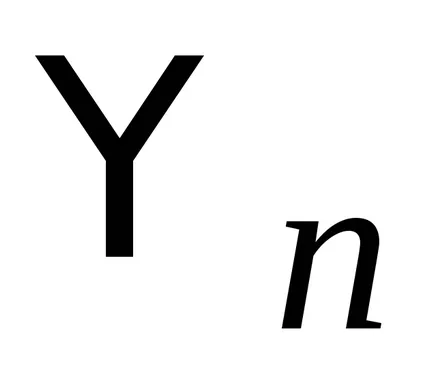
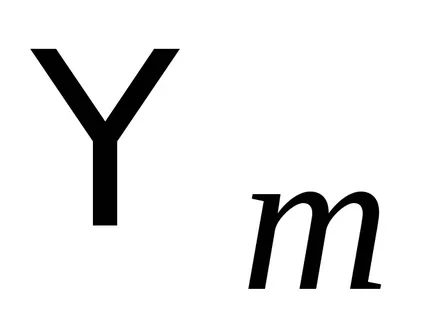

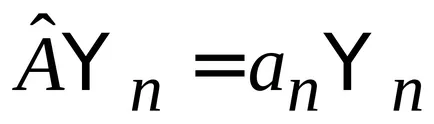
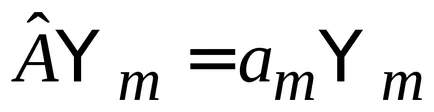
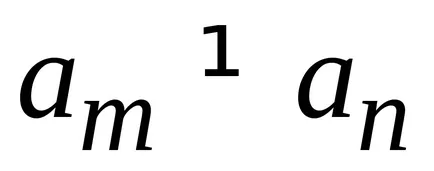
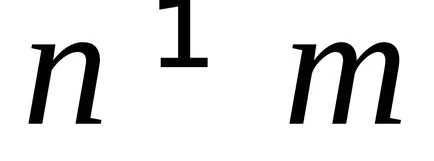
.
Като се има предвид собствените стойности са реални (2.15), ние откриваме
.
при
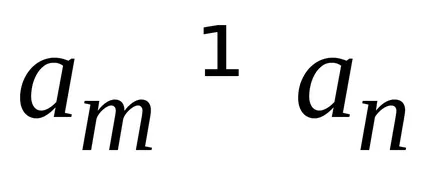
Следователно държавата
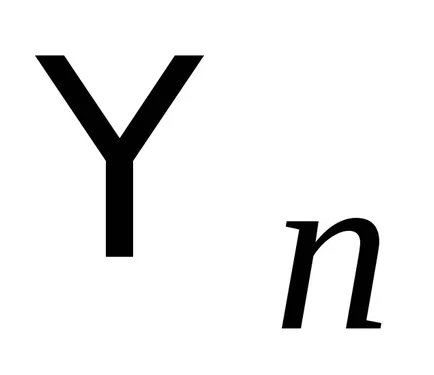
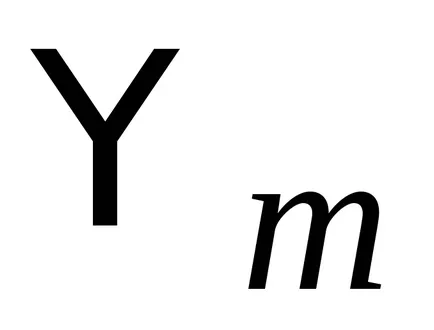
Hermitian оператор инерция
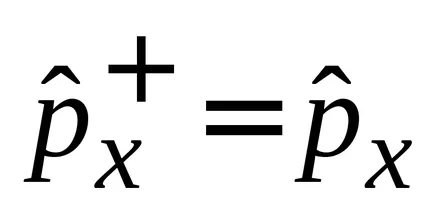
от лявата страна на оператора
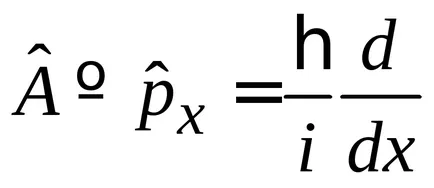
.
В дясната част на (2.14)
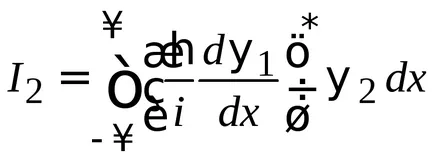
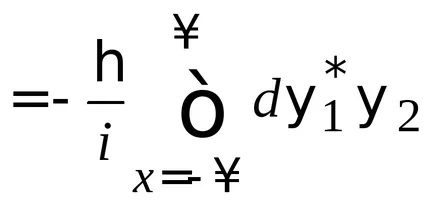
.
Функциите на вълна квадратен интегрируеми и изчезват в безкрайността, така че
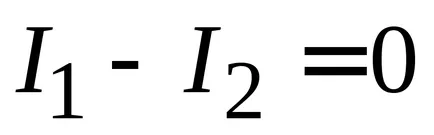
Условия orthonormality
Наборът от eigenfunctions от всякакъв Hermitian оператор

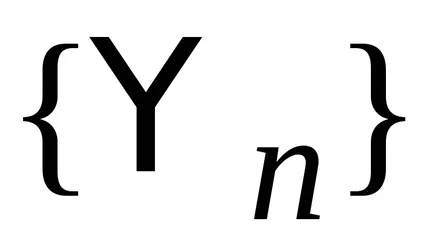

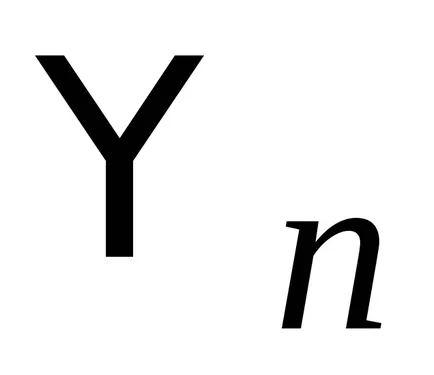
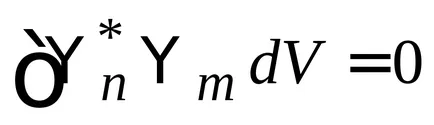
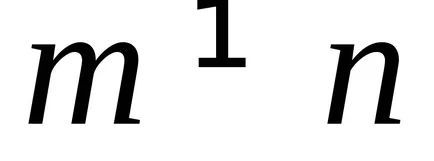
Дискретен spektrn. нормализиране
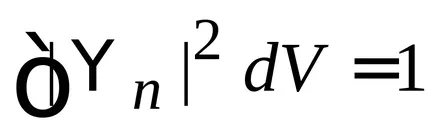
където
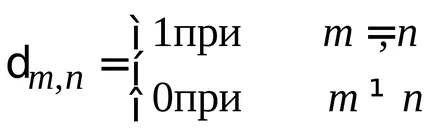
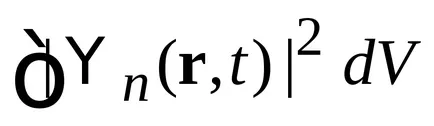
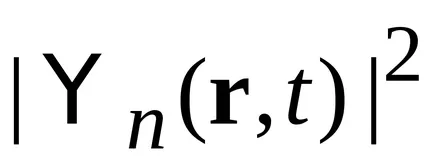
Непрекъснато spektrn. Ако индексът е със самостоятелна функция може да отнеме непрекъснати стойности, а след това (2.21), вместо символа се поставя Кронекер делта функция
при