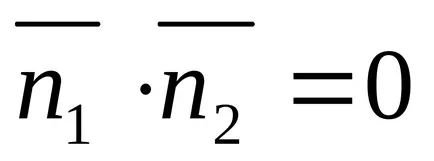Ъгълът между правите

Състоянието на паралелизъм на два реда. Да означим две линии

и.| |.

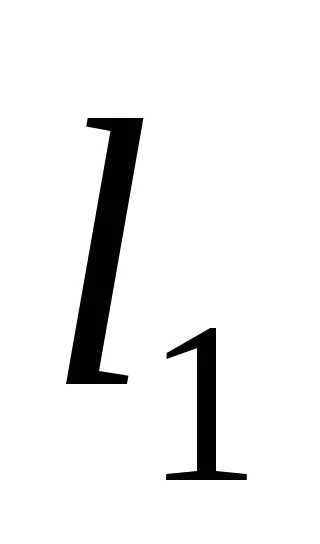
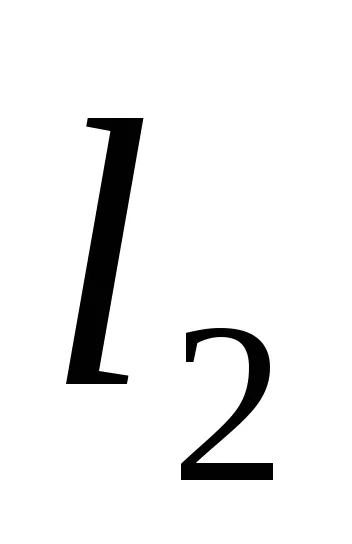
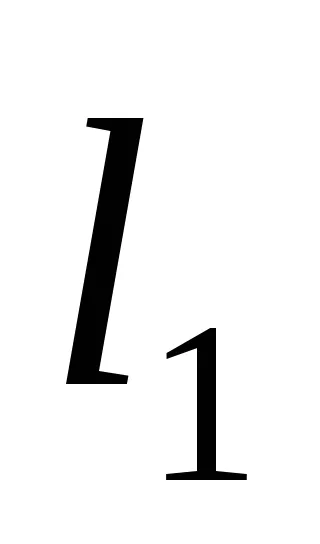
Състоянието на перпендикулярност на две прави линии:

.

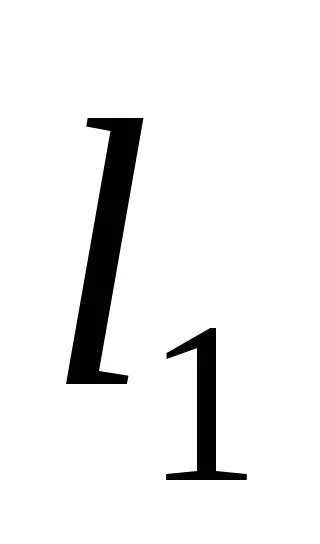
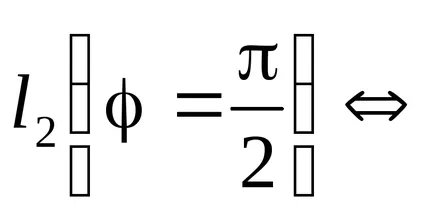
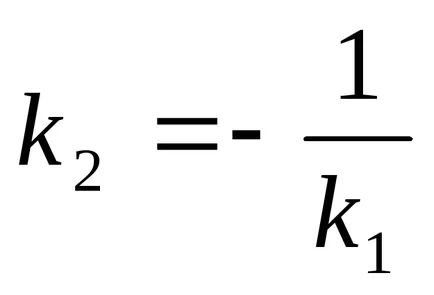
Общото уравнение на линията

Теорема. В декартовата координатна система, всеки ред се определя от уравнението на първа степен и обратно, всяка първа степен уравнение определя права линия.

Доказателство. Да предположим, че има пряка

. аконе е перпендикулярна на оста Ox, се определя от първото уравнение stepeniy = KX + б. Ако една права линия перпендикулярна на оста Ox, след това за всички точки, принадлежащи на линията се изпълнява ravenstvox = а. който също така е уравнение от първа степен.

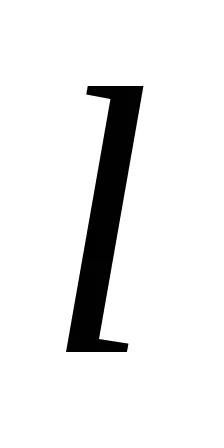
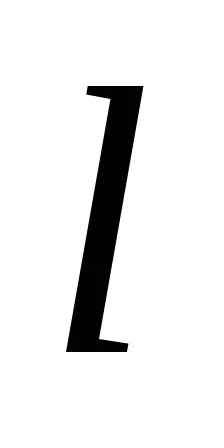
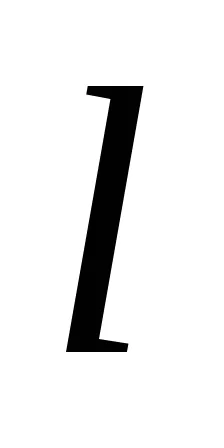
Назад. Да разгледаме уравнението

а). Ако B ≠ 0, можем да запишем

или.

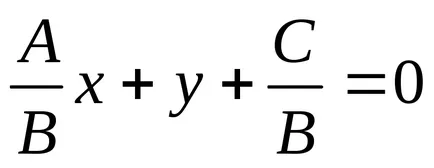
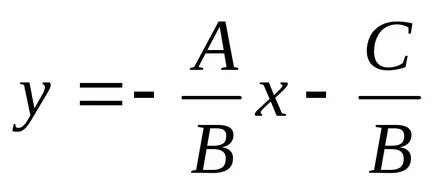
означаваме

и. след това- уравнение на линията.

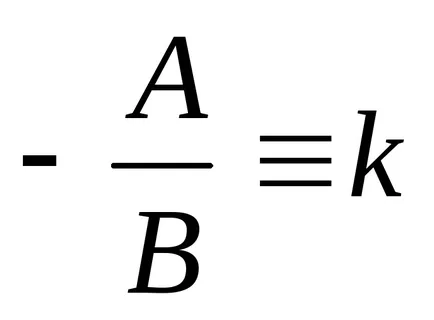
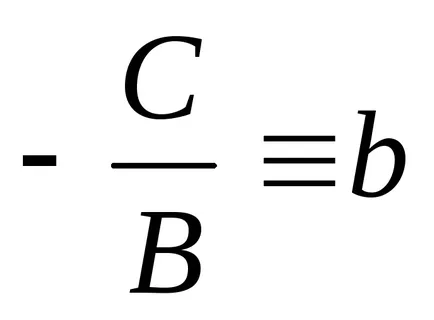
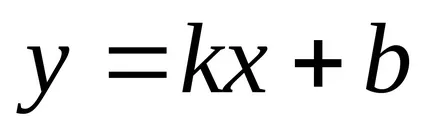
б). Ако В = 0, тогава А ≠ 0.

=> X = .

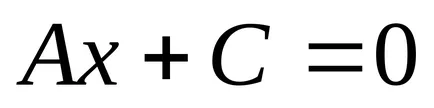
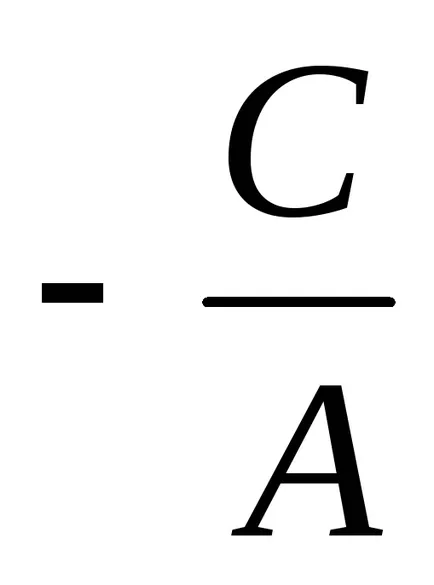
нека

≡a => х = а - уравнението на линия, паралелна на оста ОУ.

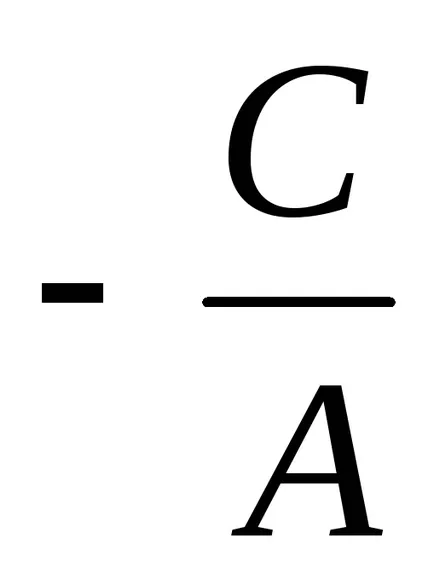
Ос на уравнение + С + С = 0 се нарича общо уравнение линия. защото тя определя всички видове линии, без изключение.

Непълно уравнение от първа степен

Помислете за три случая, когато уравнението е непълна.

С = 0 => Ах + С = 0 - линия преминава през началото.

В = 0 (А ≠ 0) => С = Ах + 0 - линия, паралелна на оста у.

A = 0 (V ≠ 0) => С + С = 0 - линия е успоредна Ox.

Уравнение на линията "на парчета"

Да разгледаме уравнението Ах + С + С = 0, gdeA ≠ 0, ≠ 0 и C ≠ 0.

тя се преобразува до Форма Ах + на С = С и разделете на (С):

уравнение на права линия в сегменти. (8)

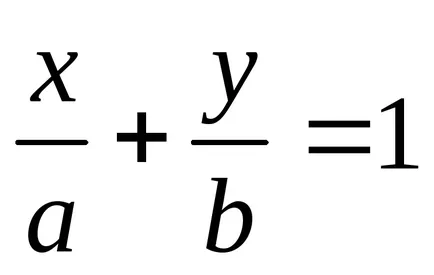
Numbers а и Ь в уравнение (8) има геометрична значение. Това е отрязъкът правата линия на координатните оси.

Разбира се. Намираме координатите на точките на пресичане с оста х:

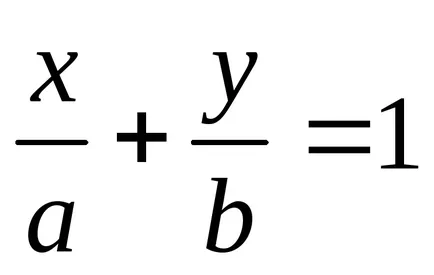
По същия начин, дължината на сегмент е отрязана от права линия на оста у.

Съвместно проучване на уравнения на две линии

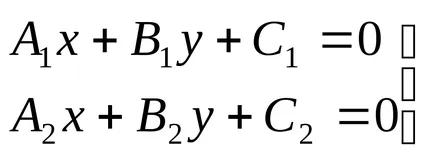
Всяка уравнение определя линия в равнината. Общият разтвор на тези уравнения определя обща точка на тези линии.

1). нека

. детерминанта на системата, системата има уникално решение.

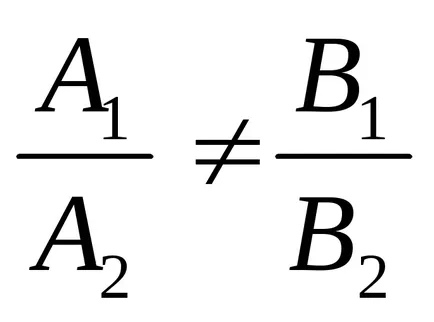
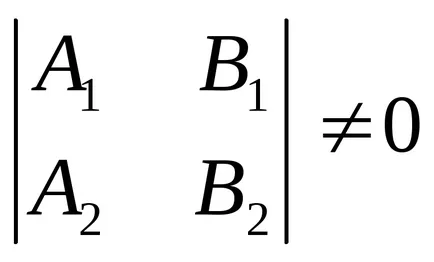
Това означава, че линиите се пресичат в една точка. Координатите на точките на пресичане са дадени от Cramer.

2). нека

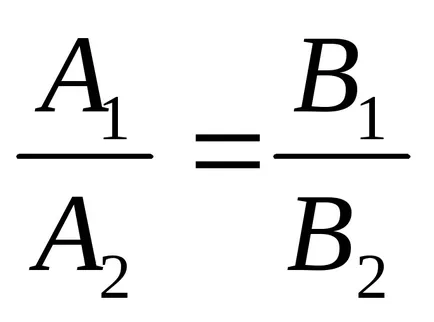
. След това има две възможности:

а)

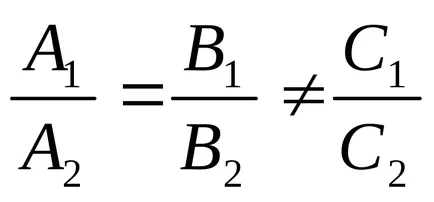
=> Не общи точки, линии са успоредни;

б)

=> Уравнение са еквивалентни, т.е. определи една и съща линия.

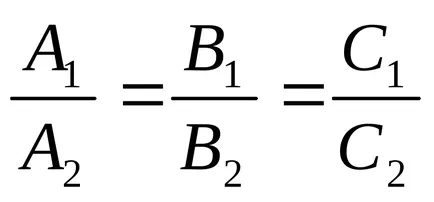
Две уравнения определят права линия, ако техните коефициенти са пропорционални.

Нормална към правата линия

Нека права линия L се дава от общото уравнение:

Нека м. M0 (x0, y0)

L. =>

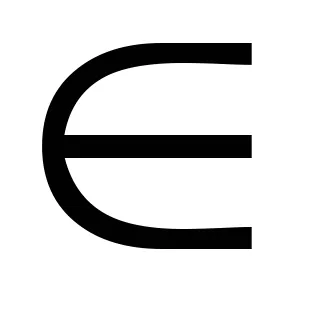
Експресия (11) може да се разглежда като скаларно произведение на два вектора:

и. защото, на, и векторНормално е да pryamoyL.

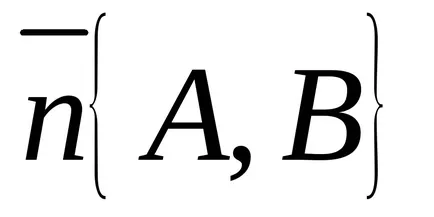
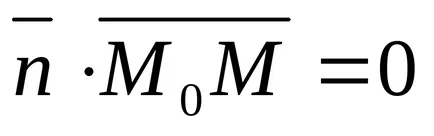
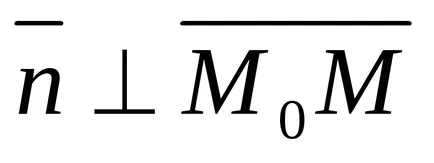
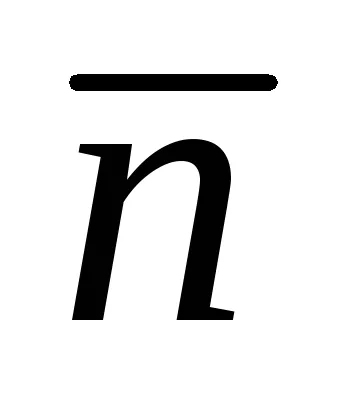
Ъгълът между две линии

Нормално на дясно:

и.

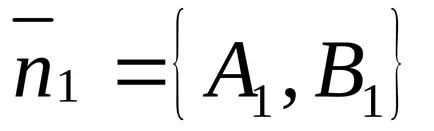
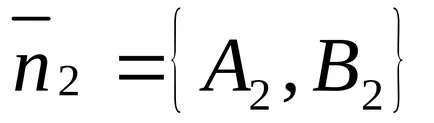
Ъгълът между редовете може да бъде определен като ъгълът между нормалните на тези линии:

След това състоянието на успоредни линии - нормално състояние на колинеарност:

.

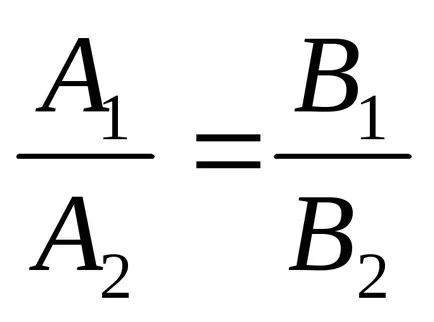
Състояние на перпендикулярни линии - е перпендикулярна нормали:

=> A1A2 + V1V2 = 0.