Геометричната смисъла на определен интеграл - studopediya

Нека един - непрекъсната функция на интервал. Тази функция не е отрицателна, т.е..

Криволинеен трапец - е

фигура, която е ограничена по-долу ос. горната графика

функция. от двете страни на вертикалните линии. ,

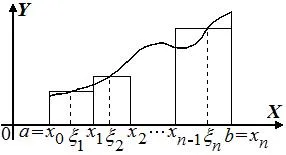
Помислете произволен дял T

Изберете точки в рамките на всеки частичен интервал на дяла. Стойността на работата функция в точка на дължината на зоната на частичен сегмент правоъгълник е геометрично с дължина основа и височина. Тогава сумата от интеграл на Риман е площта на крачка фигура подобна на тази, съставена от тези правоъгълници. Когато смилане на дял, който е при. площ от стъпка фигура подобна тенденция в областта на криволинеен трапец:

Геометричната смисъла на определен интеграл.

В определеният интеграл от неотрицателна непрекъсната функция

на интервал равна на площта на кривата трапец лежи под графиката на тази функция.

Понякога е възможно да се изчисли определен интеграл се използват само геометричния му значение.

Пример 1. Изчислява се интеграл.

В подинтегрален е непрекъснат и положително върху интервала

. Togdavelichina неразделна фигура е площта под графиката на функцията. Тази цифра е обичайната трапец площ формулата на трапец намерите

Пример 2. Изчислява се интеграл.

Подинтегрален е непрекъсната и неотрицателна в интервала. Togdavelichina неразделна фигура е площта под графиката на функцията. Тази цифра е с радиус една четвърт кръг.

До кръг площ формула, ние откриваме, че стойността на интеграла