Формули и свойства на четириъгълници
H не след студенти и преподаватели по математика и може да намерите най-основните свойства и формули четириъгълници площади, изучавани в училището на основната програма. Редовно се използват тези теоретични познания по темата и преглед на уроците на геометрия (планиметрия) и като подготовка за изпита по matematkie. Всички математически понятия и факти, са илюстрирани с цвят подчертава основните характеристики се изучават.
1) Square четириъгълници
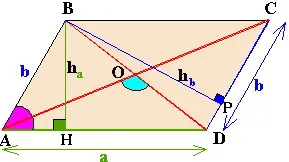
продуктова база, а височината
poroizvedenie страни на синуса на ъгъла между тях
poluproizvedenie диагонали на синуса на ъгъла между тях
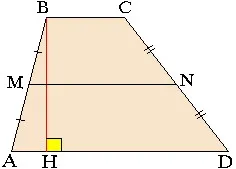
работи на половин работен сума от височината на базите
произведението на височината на централната линия
poluproizvedenie диагонали на синуса на ъгъла между тях
Площта на всеки четириъгълник
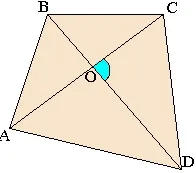
Площ на произволен четириъгълник poluproizvedeniyu диагоналите равни на синуса на ъгъла между тях
2) Свойства на успоредник
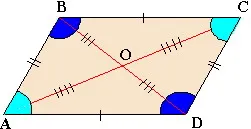
противоположните страни и ъгли са равни
диагонали се пресичат в точката на пресичане и разполовявам
3) сумата от квадратите на диагоналите на успоредник е равна на сумата от квадратите на страните, т.е.
3) Средно в линията на трапец
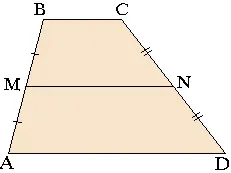
Теорема на средната линия: Близкия линия, успоредна на основите на трапец и е равна на половината на сбора от тях.
Това означава, че
4) средната линия е равнобедрен трапец

Срединната линия на равнобедрен трапец е равна на по-ниската база на отсечката, свързваща основата до върха на височината на увиване привлечени към него.
5) теорема да смени диагонално трапец
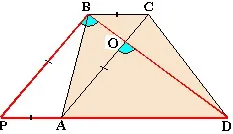
Теорема: Ако трапеца през горния В, както е показано в ляво. да проведе паралелна секция на един от диагоналите, то ще се сбъдне следните факти:
Keystone - равнобедрен равнобедрен
6) Четири забележителен точка на трапеца
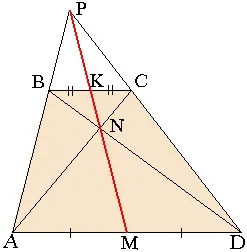
Теорема: Във всеки един момент на пресичане на диагоналите на трапеца, точка peersecheniya продълженията страни и по средата на основание лежат на една права.
Това е точката на М, М, К и Р са колинеарни
Kolpakov Александър Николаевич. Математика учител.
Александър, разбира се, има много джобни наръчници, НО! Би било готино да се направи за преподаватели по математика изтеглени материали във всеки удобен формат, както и на конкретните задачи на такива мамят лист отново от простото към комплекса.
Тази добра селекция, по мое мнение, липсата на информация за ъглите, например, две вътрешни ъгли на успоредник, свързани от една страна, се добавят до 180 градуса.
По принцип, ако формулата на площада диагонално да предприеме по-малък ъгъл между тях? Или може ли някой?
Александър, ако не и по-трудно, ще се радва да получи файл към електронна поща или свят tyknut препратка към него. За по-рано много благодарни за задачата титанична.