Формула на двойно аргумент

§ 24. Формула двойно аргумент

Тук ние ще се съсредоточи върху формулите на тригонометрията, ни дава възможност да изразят тези формули обикновено се нарича двойно аргумент. Името може да бъде, не е много добра, тъй като, наистина, и имена като "формула, за да донесе", "задължително сума", "косинус от разликата", и т.н., но това не е от значение: най-важното, че има вербална символ което позволява посветена да се разбере какво е заложено на карта.
Разглеждане на експресия sin2h, подаване на 2 под формата на х + х. Това ще позволи да се прилага експресионен грях (х + х) формулата "задължително сума" (вж. § 21). В момента има:

Разглеждане на експресия sos2h, подаване на 2 под формата на х + х. Това ще позволи да се прилага за експресия на COS (х + х) формулата "косинус сума" (вж. § 21). В момента има:

Разглеждане на експресията TG 2, представящ в същото време под формата на 2 х + х. Това ще позволи да се приложи изразяване Tg (х + х) формулата "допирателна сума" (вж. § 23). В момента има:

Формула "задължително двойно аргумент" и "косинус двойно аргумент" валидна за всички аргументи стойности (няма ограничение), докато формулата "допирателна двойно аргумент" валидна само за тези стойности на аргумент X, които са определени TG х и TG 2 X, и също е нула знаменател, т.е.
Разбира се, формулата на двойно аргумент може да се прилага в случаите, когато положението на аргумент х отнема по-сложна експресия. По този начин, следните зависимости:

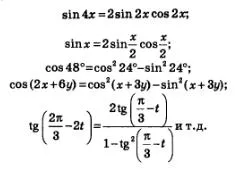
И, както винаги, всеки от трите получени резултати в тази секция, формулите на двойно аргумент могат да се използват както за писане от дясно на ляво и от ляво на дясно. Например,

Пример 1. докаже идентичност:

Решение: а) използване на факта, че 1 х = грях 2 + 2 х COS, формулата на синуса на двойно аргумента. получаваме:

Пример 2. Намаляване на фракция
Решение. Използването на числителя доказано в Пример 1 и идентичността и знаменател - двойно косинус аргумент формула. получаваме:

ПРИМЕР 3. Изчислете:
Решение: а) Спецификация израз представлява от дясната страна на двойно аргумент косинус. Виждайки това, ние получаваме

б) набор израз е от дясната страна на двойно синуса на аргумента, но само липсва множител 2. Въведете го, получаваме:

в) Този пример е много по-трудно, но това е по-красива от предишната: необходимо е да се отгатне умножение и деление на даден израз на 4sos18 °. Какво ще я дам? Виж:

Както можете да видите, ние сме два пъти използва формулата на задължително на двойното аргумент. За да събере изчисляването до края, ние се отбележи, че 72 ° = 90 ° -18 °. Така че, грях 72 0 = грях (90 ° -18 0) sos18 = 0. По този начин,

Пример 4. За да се докаже идентичност
Решение. Трансформация в лявата част на необходимата идентичност:

Увеличаването както на числителя и знаменателя на последната фракция 2 ( "персонализиране" знаменателя на формулата на синуса на двойно аргумента), ние получаваме:

Така че това, което искахме да докажем.
Забележка. За пореден път привлече вниманието ви към факта, че идентичността е доказано само за допустимия стойността на х, по-специално за
за стойностите на х, за които наличните знаменателите не са нула.
Пример 5. знаейки, че

Решение: а) се използва формула X 2 + грях COS на 2 х = 1. Ние имаме:

б) За да се изчисли sin2h използване формула грях 2 = грях 2 hsoz х.
Cos Х-стойност, дадена в състоянието, както и стойността на х грях находка следва. На първо място, ние знаем, че
На второ място, при условие х аргумент принадлежи към четвъртото тримесечие, и то задължително е отрицателна. Това означава, че от двете стойности

в) tg2h изчислява с помощта на определението на допирателната:

г) изчисляване първата употреба за задвижване на формулата:
Нанесете формулата за изразът soz4x двойни аргументи косинус soz4h 2 = защото 2 - SIN 2 2. Ние използваме факта, че стойностите на 2 и защото грехът 2xuzhe нас намерени:

Пример 6. решаване на уравнение sin4h-soz2h = 0.
Решение. Ако лявата страна на уравнението прилага за експресията sin4x формула задължително двойно аргумент, той ще бъде в състояние да се разшири лявата страна на факторизирането. Имаме последователно:

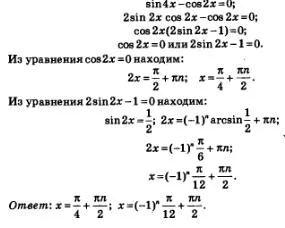
AG Mordkovich Алгебра 10 клас

Ако имате корекции или предложения на този урок, моля свържете се с нас.

Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.