Евклидово пространство и неговите свойства, описателен геометрия
Според теорията на множествата, всяка геометрична фигура трябва да се разглежда като съвкупност от всички точки, които принадлежат към нея. По този начин, всяка геометрична фигура има не-празен комплект. Показване на геометрични форми на самолет (или друга повърхност) може да бъде постигнато чрез проектиране си точка в равнината (повърхност). Препоръчително е да се помисли за евклидовата пространство и неговите свойства да учат метода на прожектиране. Свойствата на евклидово пространство могат да бъдат изразени с помощта на предлаганата система - аксиомата, че създават зависимости и връзки между елементите на пространството. Точки, линии и равнини на Euclidean пространство (триизмерни) са в определена връзка, която може да бъде определена дума, принадлежаща или честота. Срок честота замества термини като лежат на, да мине през. В бъдеще, вместо израза лежи в равнината на линията минава през точката, ние ще използваме: - буква А принадлежи на (инцидент) равнина; - B принадлежи към прав точка.
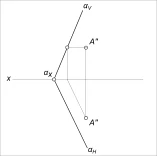
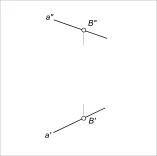
Евклидово пространство и неговите свойства
Символичното формата на тези изрази може да се запише
Аксиоми на падане или връзката между елементите, принадлежащи Евклидово пространство може да се изрази със следните изречения:
1. Ако точка А принадлежи на режисира. и линията принадлежи към равнина α. Точка, която принадлежи към равнина на алфа
\ [A ∈ на ⊂ α → A ∈ α \]
2. Два различни точки А и Б са винаги на едно и също, и само една права линия или линия на всеки принадлежи към най-малко две точки А и В
\ [(∀A, В) (А ≠ В) → (∃ 1 а) (а ∋ А, В) \]
3. Три различни точки А. В и С не принадлежат към една и съща права линия принадлежат към една и съща и само една равнина
\ [(∀ ABC) (А ≠ B ≠ С) ∧ (A, B, C ≠ ∈ а) → (∃ 1 α) \]
4. Ако две точки А и В. принадлежащи към насочи. принадлежат към равнина α. след това права линия принадлежи към равнината α
\ [(∀ АВ) (А ≠ В) (А, В ∈ а) ∧ (A, B ∈ α) → (а ⊂ α) \]
В допълнение към тези предложения, може да бъдат формулирани други предложения, принадлежащи към елементите на пространството Euclidean.
5. Две линии, които принадлежат към една и съща равнина, могат да принадлежат на една точка, но това не може да бъде.
6. Две равнини могат да принадлежат към една и съща права линия, но това не може да бъде.
7. самолета не са част от него направо могат да принадлежат към една точка, но това не може да бъде.
Последните три съществени предложения перифразират аксиома на паралелизъм: - Предложение 5 постановява, че в евклидовата равнина две прави или да се пресекат, (собственост на една точка), или нямат обща точка - те се наричат паралелно в този случай; - Твърдение 6 казва, че в Euclidean пространство на две равнина или се пресичат (принадлежат към една и съща линия), или те са успоредни. - предложение 7 се посочва, че в евклидово пространство права линия не принадлежи на самолета, или да я пресича (и равнини принадлежат към една и съща точка), или са успоредни.