Билет по висша математика
Нанесете една проста смяна в зависимост от характеристиките и вида на подинтегрален.
1) Когато R (х -sin, COS х) = - R (син х, COS х). рационализира заместване защото х = Т.
2) Ако R (син х, - защото х) = - R (син х, COS X). рационализира заместване грях х = Т.
3) Ако R (-sin х, - COS х) = R (х грях, COS х). рационализира заместване TG х = Т. Това заместване се прилага и ако е интеграл на формуляра R (TGX) DT
следните замествания се използват, когато намирането на интеграл от типа:
Sinx = Т, ако п - цяло число, положително нечетно число
Cosx = Т, ако m - цяло число положително нечетно число
TGX = Т, ако m + п - дори, отрицателно число
Ако m и п - цяло число, не-отрицателни четни числа, след това се използва формулата за намаляване на ред:
Намирането на интеграл от най-простите видове ирационално функция (където А, В, С, D - естествени числа; # 945; # 946; # 947; # 948; - естествено число). Това неразделна се редуцира до неразделна на рационално funktsiis чрез заместване на (брадва + б) (СХ + D) = TK. където к - най-малкото общо кратно # 945; # 946 ;, ..., # 948; # 947;
Свойствата на определен интеграл:
За функция у = е (х). определен при х = а. равенство.
Това означава, че стойността на определен интеграл със същите граници на интеграция, равни на нула. За интегрируеми на интервала [а; Ь] функция се изпълнява.
С други думи, при смяна на горните и долните граници на интеграция сайтове стойност на определен интеграл е наопаки.
4. постоянен фактор може да се приема като знак на определен интеграл. ,
6. Ако функция у = F (х) е интегрируеми на интервала [а; Ь] за всяка стойност на аргумента, след това.
8. средна стойност теорема: С € [а, б],
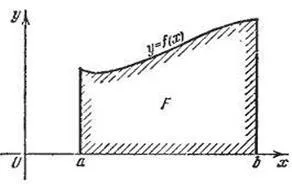
Площта на криволинеен трапец е числено равна на определен интеграл
Ако извита трапец е разположен под оста Ox, S = -
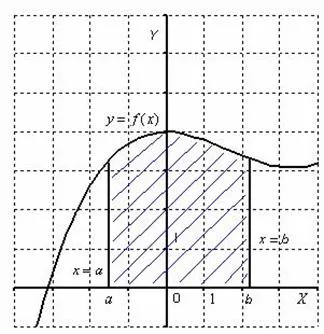
Площта на фигурата, ограничена от кривите у = е (х), у = грам (X), така че е (х)<=g(x), находится по формуле:
При изчисляване на областта на криволинейна трапец, в случай, когато горната граница се определя от параметрични уравнения ш (т)> = 0, т € [t1, t2], прави линии х = А, X = б, тогава
(Вместо # 945; и # 946; - Т1, Т2, вместо # 966; и втори боклук - х, у)
(Вместо р - с)
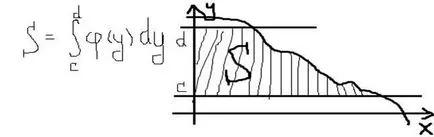
Ако извити трапец, ограничена от х = крива # 966; (Y) прави линии Y = С, Y = г, оста OY:
Методи за изчисляване на определени интеграли:
Методът за интегриране по части: Нека интервала [а; Ь] са дефинирани и непрекъсната функция ф (х) и V (X), съгласно заглавието, с формула
метода на заместването: Нека изчисляване на интеграл от непрекъсната функция, за да се направи смяна X = # 966 (т), т € [t1, t2], DX = # 966; "(т) DT, а след това (вместо # 945; и # 946; - Т1 и Т2)
Диференциално уравнение е уравнение на формата, където - функцията дефинирани в област на пространството, - независима променлива, - функция на - производни от тях.
Редът на уравнението се нарича най-високите производни на поръчки, включени в уравнението.
Контролирайте първия ред: F (X, Y, Y '), ако това е позволено по отношение у ", а след това тя ще изглежда. т. За. Y '= dydx, ди = Y' DX.
dydx = F (х, у); Dy = F (х, у) DX
Проблемът с Коши за първи ред на контрол: контрол на първия ред, за да се намери решение, което отговаря на първоначалното състояние, х = x0, у = y0, тоест, да намерите неразделна крива, минаваща през точката (x0, y0) ...
Общият разтвор на диференциални уравнения на формата е функция у = F (х) + С, както е определено в област, ако отговаря на следните условия:
1. За всяка стойност на С е разтвор на уравнението F (х, у, у) = 0
2. За началните условия (X0, Y0) € D съществуват стойности на С, които съществуват уравнение Y0 = F (x0, С)
Самостоятелно контролен разтвор - всеки разтвор, който е получен от общата стойност за определен S.
(М и N се заменя от Р и Q)
Контрол с множество променливи:
- Контрол с разделящи се променливи.
Решение: Разделяне с M2 (х) * N1 (у), ние получаваме уравнението
Интегриране, получаваме: + - обща неразделна
F функцията (х, у) се нарича хомогенна функция на степен к, ако идентичността е изпълнено на всички т. Например, функцията - хомогенна втора степен, че да ...
Контрол хомогенна ако F функция (х, у) е нулев порядък хомогенна функция.
Еднакво контрол често разположен в диференциална форма, където М и М - хомогенни функции на същия ред.
Решение: хомогенна уравнение се трансформира в уравнение с делими променливи от заместването: у = ф * X, Y '= ф' + х '* ф, ди = + xdu udx, ф = YX
- линеен контрол първи ред
Имоти: неизвестна функция у продукт и производните му у ", включени във формулата 1 степен не се размножават помежду си.
Решение: Уверете се замяна, където - функцията на х.
От тогава, след заместване в оригиналната уравнението, получаваме
Групирането на термини, които получаваме уравнението
От уравнението, получаваме V и да го замени инча
Да предположим, тогава ние се получи. Следователно получаваме U .. Да предположим, тогава функцията - общото решение
диференциално уравнение, където - функцията на определени и непрекъснато в продължение на определен обхват, - Бернули уравнение.
Решение: Уверете се подмяна и и да реши, както и линеен контрол.