Безплатна ос и централната ос на инерцията
За да се поддържа фиксирана позиция в пространството на твърда ос на въртене на тялото, е механично фиксиран, обикновено се използва лагери, т.е. на влиянието на външни сили. Въпреки това, има на оста на въртене на телата, които не променят своята ориентация в пространството без намесата на тези външни сили. Тези оси се наричат свободни оси. Това може да бъде доказано, че всяко тяло има три взаимно перпендикулярни оси, минаваща през центъра на маса, които са свободни. Тези оси се наричат също основните оси на инерцията.
В момента жироскопи, наречена много широк клас от устройства, които използват повече от сто различни случаи и физически принципи. В тази лаборатория, ние изучаваме класическата жироскопа, наричан просто жироскоп.
Жироскоп (или отгоре) е симетрична масивно тяло въртяща се с висока ъглова скорост около оста на симетрия. Това ще се нарича ос на оста на жироскоп. Жироскоп ос е една от основните оси на инерция (свободна вал). Момент жироскоп импулс в този случай е насочено по оста и е равно на L = I.
Помислете за хоризонтално ориентиран балансиран жироскоп (центърът на тежестта се намира над центъра на въртене). От момента на тежестта за това е нула, а след това, според закона за запазване на момента на импулса L = I = конст, т.е. посока на нейната ос на въртене не се променя положението в пространството.
Когато се опитате да доведе до оста на въртене на жироскопа се наблюдава явление, наречено жироскопичен ефект. Същността на ефекта: silyF под действието прилага към въртящата ос на жироскопа, ос жироскоп се върти в равнина, перпендикулярна на тази сила. Например, когато действието на вертикалната сила, ос жироскоп се върти в хоризонталната равнина. На пръв поглед това изглежда неестествено.
Жироскопични ефект се обясни по следния начин (Фигура 5). В момент М на сила F насочена перпендикулярно на оста му, като М = [г, F]. R-радиус вектор от центъра на масата на жироскопа до точката на прилагане на сила.
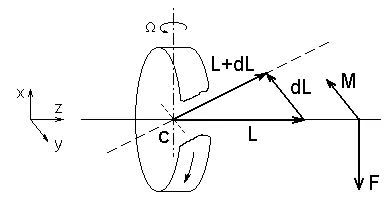
През DT момент жироскопичен импулс L се увеличава дл DT = М * (съгласно основния закон на въртеливо движение) и насочена в същата посока, като М, и става равна на L + дл. L + дл посока съвпада с нов посоката на въртене на оста на жироскоп. Така оста жироскоп върти в равнина, перпендикулярна на сила F под определен ъгъл dφ = | дл | / L = М * DT / L, с ъглова скорост
Ъгловата скорост на въртене на ос жироскоп наречени прецесия ъглова скорост, и въртеливо движение ос жироскоп прецесия.
М. L. вектори перпендикулярни една на друга, така че може да пише
Тази формула се получава, когато М. L. вектори са взаимно перпендикулярни, но може да се докаже, че следните притежава в общия случай.
Имайте предвид, че данните и изходни аргументи формули важи в случаите, когато въртенето ъглова скорост на на жироскоп >> .
От (9) следва, че степента на прецесия пряко пропорционална на М и обратно пропорционална на момент жироскоп L. Ако времето на импулса на действие на силата е малък, ъгловата скорост L е достатъчно голям, скоростта на прецесия бъде малък. Ето защо, в краткосрочен план за действие на силите на практика не се променя ориентацията на жироскопа оста на въртене в пространството. За неговата промяна трябва да се прилага сила за дълго време.