3-9 обръща произволна ос в пространството

3-9 върти около произволна ос в пространството

Общата обрат в разследването около произволна ос в пространството е често срещан, като роботиката, анимация, моделиране. Следвайки логиката на предходната дискусия, въртенето около произволна ос в пространството се извършва с помощта на обикновен транспорт и въртене около координатните оси. От въртенето около метода на координатна ос е известно, основната идея е да се комбинират произволно ос на въртене с една от координатните оси.

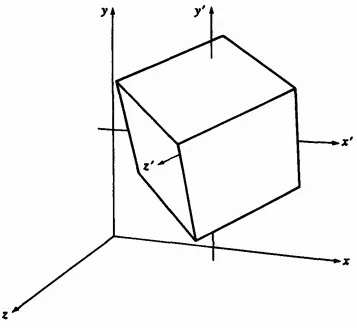
Фиг. 3-6 няколко завъртания по отношение на локалната координатна система.

Да предположим, че произволна ос в пространството преминава през насочен вектор. Въртене около тази ос на определен ъгъл съгласно следното правило:

- извършване на трансфер, така че въпросът е в системата на произход;

- изпълнява подходящи обороти, така че оста на въртене съвпада с оста;

- да се върти под ъгъл около оста;

- извършване на преобразуване обратен на този оставя да се комбинират с оста на оста на въртене;

- изпълни обратния превод.

Като цяло, до произволна ос, преминаваща през началото съвпада с една от координатните оси, е необходимо да се направи две последователни люлеене около другите две оси. За комбиниране произволна ос на въртене с оста на въртене на първата извършва около ос и след това около оста. За да се определи ъгълът на въртене около оста, използвани за превръщането на произволна ос в равнина, да се проектира първата употреба равнина на ос единичен вектор (фиг. 3-7a) на. Компоненти и прогнозния вектор равни - -components и посока единичен вектор на оста на въртене.

Фиг. 3-7a, следва, че

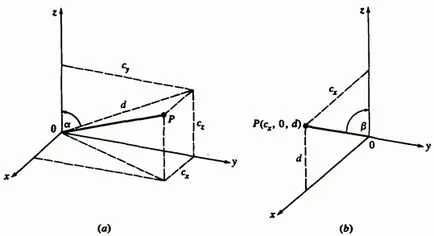
Фиг. 3-7 превръща необходима за привеждане в съответствие с вектор ос единица. (А) на въртенето около; (В) се завърти.

След превод на равнината чрез завъртане около оста, компонент на вектора на единица е равна и равно-компонент, т.е. -component посока вектор, както е показано на фиг. 3-7b. Дължината на вектора на единица е, разбира се, 1. Така, ъгълът на въртене около оста желания за комбиниране произволна ос с ос, равно на

След пълна трансформация може да се запише като

където матрицата транспорт

въртене около ос матрица трансформация

И накрая, на въртене около произволна ос на въртене се определя от матрицата около ос

На практика, ъгли, и не са изчислени изрично. Елементите на матрицата за въртене и (3-21) са получени от уравненията (3-18) - (3-20) чрез извършване на две операции на разделяне и квадратен корен. Въпреки че тези резултати са разработени за произволна ос в първи квадрант, те са приложими във всички квадранти.

Ако компонентите на вектора посока на произволен непознат ос, а след това, знаейки, че втората точка по оста, те могат да се определят въз основа на нормалната вектора свързване на първия и втория условия. По-точно, на оста на вектор, равен на

Нормализиране осигурява компонентите на вектора посока:

Повече напълно този метод е илюстриран в следващия пример.

Пример 3-10 Въртенето около произволна ос

Да разгледаме един куб с пресечен ъгъл е показано на фиг. 3-8a. Координатна вектори на върховете са

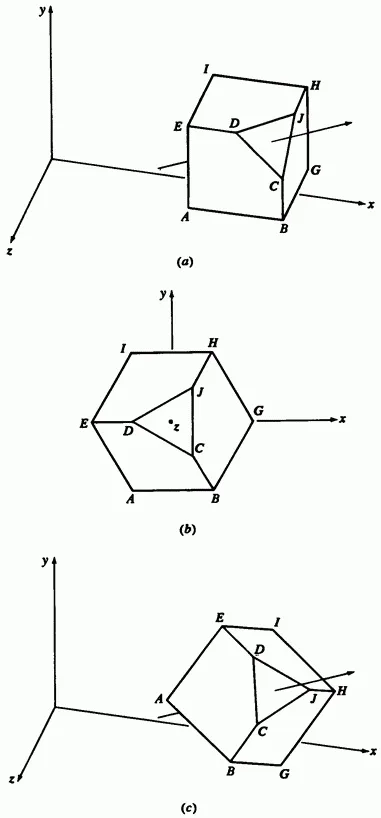
Фиг. 3-8 въртене около произволна ос.

Cube трябва да се върти около ос, минаваща през точката и противоположния ъгъл по диагонала. Ос е насочена от точката на противоположния ъгъл и минава през центъра на ръба на крилото.

Първо определят единица векторни компоненти на направляващата ос на въртене. Като се има предвид, че под ъгъл рязане триъгълник също лежи на оста, от (3-26), които

С помощта на уравнение (3-18) - (3-20) получим

Тъй като точката лежи на оста на въртене на матрицата за прехвърляне е

След това матрицата на въртене, комбиниране на произволна ос на въртене на ос, са от вида:

Inverse матрица, и се получават чрез заместване на стойностите на ъглите и, съответно, в уравнение (3-22) - (3-24).

Трансформираните координатите са междинни

Това междинно съединение резултат е показан на фиг. 3-8b. Имайте предвид, че въпросът е равен.

Ротация около произволна ос сега е равностойно на завъртане около оста си. Следователно (вж. (3-7)),

В трансформира обекта се върна на мястото си "оригинал" място в пространството с помощта на трансформация

Този резултат може да се получи чрез контактуване и комбиниране матрици съставна или лечение на самата матрица. Имайте предвид, между другото, че представляват само ротации. Горен ляв е точно транспониране -submatrix горния ляв подматрици.

Координатите за резултатите са

Фиг. 3-8С показва преобразуваната обект.